Question 1185051: A ladder is 25 cm long leans against a vertical wall so that the base of the ladder
is 7 m from the foot of the wall. If the top of the ladder slides 4 m down the wall,
by how many meters will the base of the ladder move away from the foot of the
wall?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A ladder is 25  meters long leans against a vertical wall so that the base of the ladder meters long leans against a vertical wall so that the base of the ladder
is 7 m from the foot of the wall. If the top of the ladder slides 4 m down the wall,
by how many meters will the base of the ladder move away from the foot of the wall?
~~~~~~~~~~~~~~~~~~~~~~
In this problem, you have two right angled triangles, both with the hypotenuse of 25 meters,
which represents the ladder.
In the first ladder's position, horizontal leg is 7 meters; hence, vertical leg is
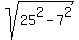 = = 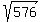 = 24 meters long.
When the ladder changes his position, sliding vertically 4 meters down, new vertical leg is 24 - 4 = 20 meters long.
Hence, new horizontal leg is = 24 meters long.
When the ladder changes his position, sliding vertically 4 meters down, new vertical leg is 24 - 4 = 20 meters long.
Hence, new horizontal leg is  = = 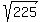 = 15 meters long.
It is the new position of the base of the ladder.
So, we just solved the problem and obtained the ANSWER: the base of the ladder will move by 15 - 7 = 8 meters. = 15 meters long.
It is the new position of the base of the ladder.
So, we just solved the problem and obtained the ANSWER: the base of the ladder will move by 15 - 7 = 8 meters.
Solved.
|
|
|