|
Question 1184949: Bryan baked a total of 1060 chocolate puffs and strawberry puffs. After giving away an equal number of both types of puffs, he was left with 2/7 of the chocolate puffs and 1/5 of the strawberry puffs. What was the total number of puffs left?
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52890)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Bryan baked a total of 1060 chocolate puffs and strawberry puffs.
After giving away an equal number of both types of puffs, he was left with 2/7 of the chocolate puffs
and 1/5 of the strawberry puffs. What was the total number of puffs left?
~~~~~~~~~~~~~~~~~
When I solve such problems, I always try to find the simplest way to solve - - - and the best way to teach.
Regarding this problem, it can be easily solved using two simple equations instead of three;
this way is simpler and, THEREFORE, is more preferable.
Let c be the number of chocolate puffs, and
let w be the number of strawberry puffs.
The total was 1600 puffs, which gives you first equation
c + w = 1600 (1)
After giving away, Bryan was left with 2/7 of the chocolate puffs; hence, he gave away 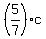 chocolate puffs.
He was left with 1/5 of the strawberry puffs; hence, he gave away chocolate puffs.
He was left with 1/5 of the strawberry puffs; hence, he gave away 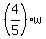 strawberry puffs.
He gave away equal number of both types of puffs; it gives you second equation strawberry puffs.
He gave away equal number of both types of puffs; it gives you second equation
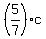 = = 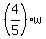 . (2)
Multiply equation (2) by 35 (both sides). You will get then
25c = 28w. (3)
Now you have the system of two equations (1) and (3).
From (1), express c = 1060-w and substitute it to equation (3). You will get
25*(1060-w) = 28w
25*1060 - 25w = 28w
25*1060 = 28w + 25w
w = . (2)
Multiply equation (2) by 35 (both sides). You will get then
25c = 28w. (3)
Now you have the system of two equations (1) and (3).
From (1), express c = 1060-w and substitute it to equation (3). You will get
25*(1060-w) = 28w
25*1060 - 25w = 28w
25*1060 = 28w + 25w
w =  = 500.
So, originally, there were 500 strawberry puffs and 1060-500 = 560 chocolate puffs.
Hence, the total number of puffs left was = 500.
So, originally, there were 500 strawberry puffs and 1060-500 = 560 chocolate puffs.
Hence, the total number of puffs left was  + +  = 2*80 + 100 = 260. ANSWER = 2*80 + 100 = 260. ANSWER
Solved and thoroughly explained.
Answer by greenestamps(13209)   (Show Source): (Show Source):
|
|
|
| |