SOLUTION: Given two specific terms of geometric sequence. Find the common ratio and first term. Show the solution. a(2)=4 ; a(5)=32 please can you teach me the step by step because

Algebra ->  Sequences-and-series -> SOLUTION: Given two specific terms of geometric sequence. Find the common ratio and first term. Show the solution. a(2)=4 ; a(5)=32 please can you teach me the step by step because       Log On


   

Question 1184936: Given two specific terms of geometric sequence. Find the common ratio and first term. Show the solution.

a(2)=4 ; a(5)=32
please can you teach me the step by step because I really can't understand T-T
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625) About Me  (Show Source):
You can put this solution on YOUR website!
You see that three ratios are between those two terms. You should also be familiar with the few lower powers of 2.

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
Given two specific terms of geometric sequence. Find the common ratio and first term. Show the solution.

a(2)=4 ; a(5)=32
please can you teach me the step by step because I really can't understand T-T
The easiest method is to calculate r, or common ratio:  
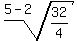This becomes: root+%285+-+2%2C+32%2F4%29, and then: matrix%281%2C3%2C+root+%283%2C+8%29%2C+%22=%22%2C+2%29

With common ratio being 2, and using the 2nd term, 4, we get: 

                                                First term or highlight_green%28matrix%281%2C3%2C+a%5B1%5D%2C+%22=%22%2C+2%29%29

OR

The LONGER method:
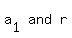Use the equation for a term of a GP, which is: matrix%281%2C3%2C+a%5Bn%5D%2C+%22=%22%2C+a%5B1%5Dr%5E%28n+-+1%29%29, and the 2nd term (4) to find an equation in matrix%281%2C3%2C+a%5B1%5D%2C+and%2C+r%29
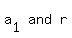Repeat the process but this time, use 5th term (32) to find an equation in matrix%281%2C3%2C+a%5B1%5D%2C+and%2C+r%29
You will then have a system of equations in 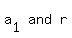matrix%281%2C3%2C+a%5B1%5D%2C+and%2C+r%29, which you then solve to get the values of the 1st term (a1), and r, the common ratio.