SOLUTION: Consider the sequence of numbers: 1,7,17,31,49,71 What is the expression for the nth term of the sequence?

Algebra ->  Testmodule -> SOLUTION: Consider the sequence of numbers: 1,7,17,31,49,71 What is the expression for the nth term of the sequence?      Log On


   

Question 1184909: Consider the sequence of numbers:
1,7,17,31,49,71
What is the expression for the nth term of the sequence?
Found 2 solutions by Edwin McCravy, greenestamps:
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
We check to see if it can be part of a polynomial sequence.
We write the sequence out:

1  7  17  31  49  71

We subtract every term from the term on its immediate right and write the
difference below and between the terms. This forms the sequence of FIRST
DIFFERENCES:

1  7  17  31  49  71
  6 10  14  18  22

Then we repeat. We subtract every term from the term on its immediate right
and write the difference below and between the terms. This forms the
sequence of SECOND DIFFERENCES:

1  7   17  31  49  71
  6  10  14  18  22
    4   4   4   4

This sequence of SECOND DIFFERENCES has all 4's. So we can find a SECOND
DEGREE polynomial expression for the nth term of the sequence:

So we assume this polynomial expression type for the nth term:

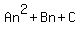t%28n%29%22%22=%22%22An%5E2%2BBn%2BC

We need to find the unknowns A, B, and C.

We substitute n=1

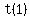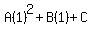t%281%29%22%22=%22%22A%281%29%5E2%2BB%281%29%2BC 

We substitute 1 for t(1) and simplify the right side:

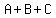1%22%22=%22%22A%2BB%2BC

The first equation of our system is

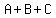A%2BB%2BC%22%22=%22%221

-----------------------

We substitute n=2

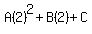t%282%29%22%22=%22%22A%282%29%5E2%2BB%282%29%2BC 

We substitute 7 for t(2) and simplify the right side:

7%22%22=%22%224A%2B2B%2BC

The second equation of our system is

4A%2B2B%2BC%22%22=%22%227

-----------------------

We substitute n=3

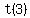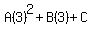t%283%29%22%22=%22%22A%283%29%5E2%2BB%283%29%2BC 

We substitute 17 for t(3) and simplify the right side:

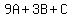17%22%22=%22%229A%2B3B%2BC

The third equation of our system is

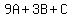9A%2B3B%2BC%22%22=%22%2217

-----------------------

We can stop here with 3 equations because we have only 3
unknowns, A,B, and C. So our system is:

system%28A%2BB%2BC=1%2C4A%2B2B%2BC=7%2C9A%2B3B%2BC=31%29

Now we solve the system of three equations in three unknowns
by substitution, elimination, echelon method, or matrix method,
and we get:

We get A=2, B=0, C=-1

So we substitute these for the nth term in:

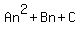
t%28n%29%22%22=%22%22An%5E2%2BBn%2BC

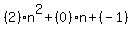t%28n%29%22%22=%22%22%282%29n%5E2%2B%280%29n%2B%28-1%29 

and simplify

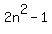t%28n%29%22%22=%22%222n%5E2-1

Edwin

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The response from the other tutor shows that the second differences for the given sequence are constant:
    1   7  17  31  49  71
      6  10  14  18  22
        4   4   4   4

The constant second differences mean the sequence can be generated by a second degree polynomial of the form

t%28n%29=an%5E2%2Bbn%2Bc

In his solution, he uses the general form of the quadratic with the first three terms of the sequence to get three equations in the coefficients a, b, and c, which he then solves.

n=1: a+b+c=1
n=2: 4a+2b+c=7
n=3: 9a+3b+c=17
...
a=2; b=0; c=-1

Here is another way to get from the constant second differences to the polynomial.

The constant difference of 4 tells us that the sequence can be generated by a second degree polynomial. But it tells us more: it tells us that the leading coefficient a is 4/(2!) = 4/2 = 2.

So the polynomial is of the form

t%28n%29=2n%5E2%2Bbn%2Bc

We can find the "bn+c" part of the polynomial by comparing the terms of the sequence to the value of 2n^2.
     n  t(n) 2n^2  difference
                  t(n)-2n^2=bn+c
   -------------------------------
     1   1     2     -1
     2   7     8     -1
     3  17    18     -1

We see that the difference between t(n) and 2n^2 is the constant -1; that means the polynomial that generates the sequence is

t%28n%29=2n%5E2-1