Question 1184860: How do I solve these questions manually (i.e. using the standardised normal distribution table) as well as on excel and python?
1. Students who have completed a speed keyboarding course have speeds that are normally distributed with a mean of 350 words per minute and a standard deviation equal to 105 words per minute. If two students were selected at random, what is the approximate probability that they would both produce less than 180 words per minute?
2. For a standardised normal distribution, determine a value, say z0, so that P(-z0 ≤ z <0) = 0.475.
3. Consider a random variable, z, that has a standardised normal distribution. Determine P(z < -1 or z > 2).
4. A random variable is normally distributed with a mean of 50 and a standard deviation of 10. If an observation is randomly selected from the distribution, what value will be exceeded 80% of the time?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you can use the following calculator to find the answer to some of these questions.
https://davidmlane.com/hyperstat/z_table.html
you also might need some additional knowledge.
my answers to the questions are shown below.
-----------------------------------------------------------
1. Students who have completed a speed keyboarding course have speeds that are normally distributed with a mean of 350 words per minute and a standard deviation equal to 105 words per minute. If two students were selected at random, what is the approximate probability that they would both produce less than 180 words per minute?
if you take one random sample, then the probability of that sample having less thn 180 words per minute is equal to .0527, based on the statistical analysis shown.
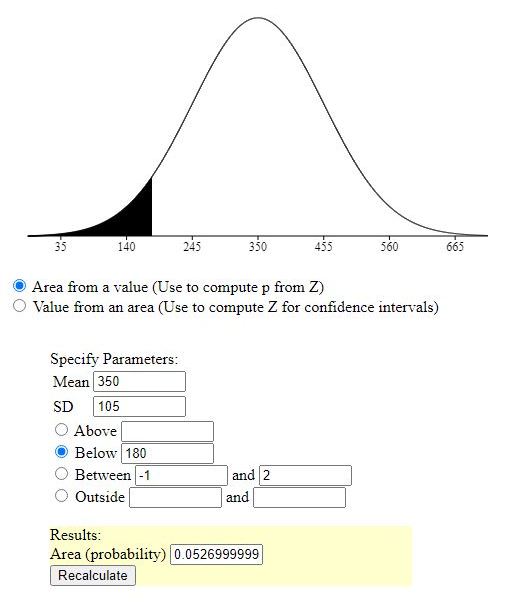
with two separate samples, taken one after the other, the probability that both would have a a score less than 180 would be approximately .0527 * .0527 = .00277729.
this assumes both samples would be independent of each other.
this also assumes a large population, so that assuming replacement versus no replacement will yield approximately the same result on the second draw.
you can round that possibility to .0028 and be very close to the actual probability, if not right on, depending on the population size.
i'm not 100% sure that this would be the correct answer, but i'm pretty sure, for whatever that's worth.
-----------------------------------------------------------
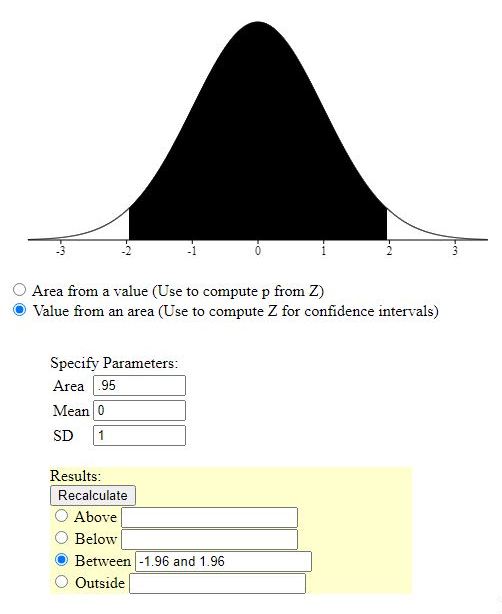
2. For a standardized normal distribution, determine a value, say z0, so that P(-z0 ≤ z <0) = 0.475.
the normal distribution is symmetric about the mean.
if you are looking for the probability of the area between the z-score of z0 and 0, then it will be half of the probability of the area between the z-score of z0 and z1.
that probability will be twice .475 = .95.
you would look for the z-scores associated with a probability of .95 between them.
the low end will be z0 and the high end will be z1.
the low end z-score of z0 will have a probability of .95/2 = .475 between that and 0.
the high end z-score of z1 will have the same probability between that and 0.
here's a look at the analysis.
first is between -1.96 and 1.96.
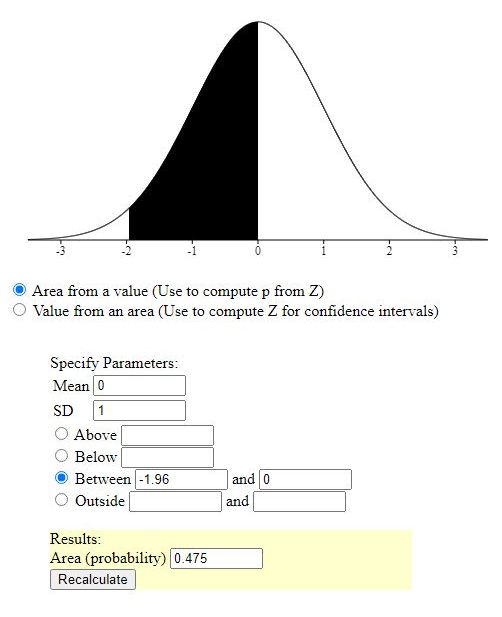
second is between -1.96 and 0.
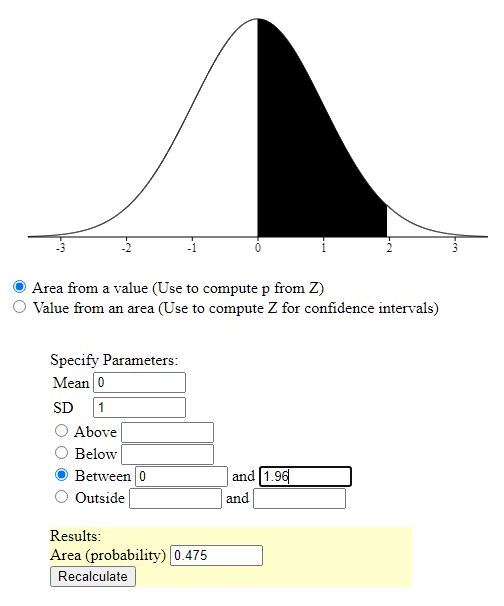
third is between 0 and 1.96.
it's the symmetry of the normal distribution that allows you to find the answer in one shot, rather than through iteration.
-----------------------------------------------------------
3. Consider a random variable, z, that has a standardized normal distribution. Determine P(z < -1 or z > 2).
this can be done directly, or indirectly, through the use of the calculator as shown below.
you can first look for the probability that -1 < z < 2.
that is shown below.
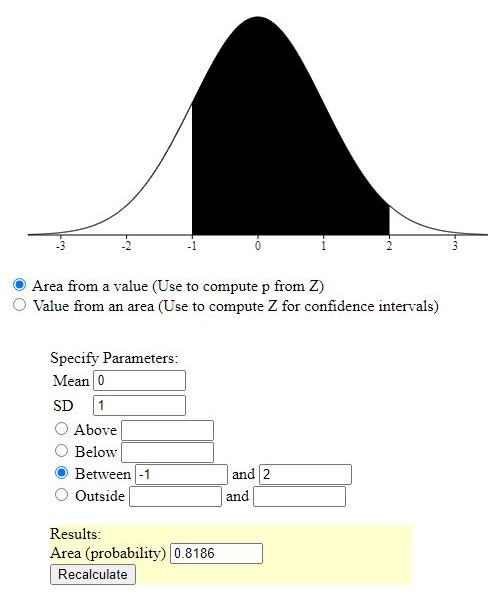
that probability is equal to .8186
since you are looking for the probability z < -1 or z > 2, then your answer would be 1 minus that = ..1814.
you can also look for the probability of the area to the left of a z-score of -1 and the probaility of the area to the right of a z-score of 2.
those probabilities would .1587 for less than z-score of -1 and .0228 for greater than z-score of 2, as shown below.
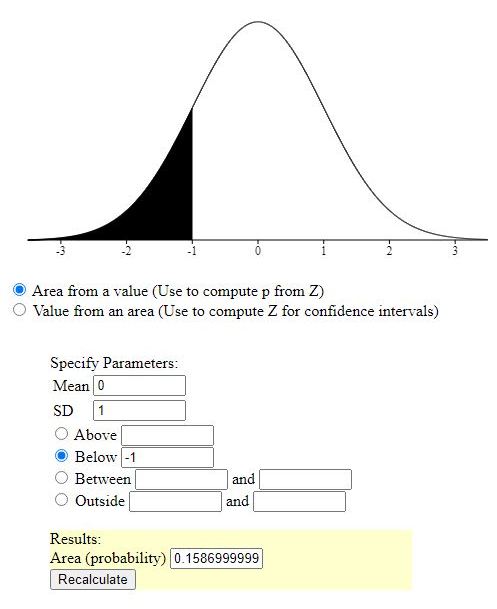
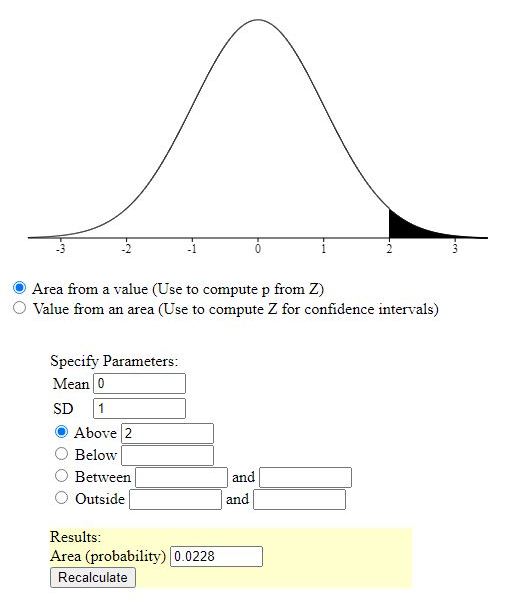
the answer would be the sum of those = .1815.
the difference between those two answers is explained by rounding.
using my ti-84 plus calculator, i get:
probability of between z-score of -1 and 2 = .8185946784
probability of less than z-score of -1 = .2596158655
probability of greater than z-score of 2 = .022750062
add the second and third results to get .1814053216
take 1 minus the first result to get .1814053216.
they're the same when the rounding is removed from the results.
-----------------------------------------------------------
4. A random variable is normally distributed with a mean of 50 and a standard deviation of 10. If an observation is randomly selected from the distribution, what value will be exceeded 80% of the time?
this can also be done directly through the use of the calculator as shown below.
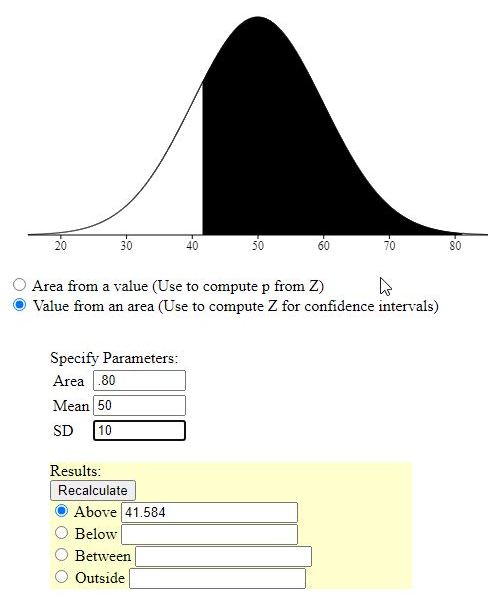
|
|
|