.
Please help me find the limit of 1/(2n+1) + 1/(2n+2) + 1/(2n+3) + ... + 1/(3n) as n goes to +infinity. Thank you!
~~~~~~~~~~~~~~~~~~~~~
Consider the sum
 =
= 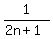 +
+ 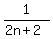 +
+ 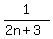 + ... +
+ ... + 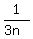 . (1)
You can write it EQUIVALENTLY in the form
. (1)
You can write it EQUIVALENTLY in the form
 =
=  . (2)
This sum is the Riemann sum for the integral of the function f(x) =
. (2)
This sum is the Riemann sum for the integral of the function f(x) = 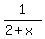 over the interval [0,1].
When n tends to infinity (n---> oo), the Riemann sum (2) tends to the integral, which is equal to the difference F(1) - F(0),
where the primitive ("antiderivative") function F(x) is F(x) = ln(2+x).
This difference F(1) - F(0) is ln(3) - ln(2) =
over the interval [0,1].
When n tends to infinity (n---> oo), the Riemann sum (2) tends to the integral, which is equal to the difference F(1) - F(0),
where the primitive ("antiderivative") function F(x) is F(x) = ln(2+x).
This difference F(1) - F(0) is ln(3) - ln(2) = 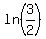 .
THEREFORE, lim
.
THEREFORE, lim  when n tends to infinity is
when n tends to infinity is 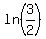 .
.
Solved.