Question 1184719: Three years ago, an engineer opened a savings account with an initial deposit of P200,000. He withdrew P50,000 three months later, and another P50,000 six months after the first withdrawal. Last year, he deposited P100,000 and withdrew P150,000 six months later. Find the account balance today if interest is 10% compounded quarterly.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website!
based on my assumptions, your account balance should be equal to $92,156.74 today, as shown in the following spreadsheet.
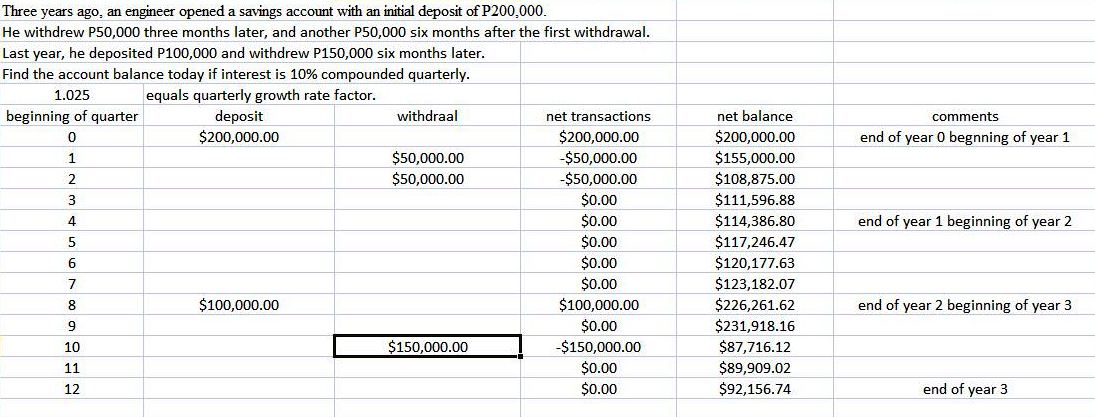
my assumptions are as follows:
> deposits and withdrawals are made at the beginning of each quarter.
> time point 0 is the beginning of quarter 1 and the end of quarter 0.
> time point 0 is also the beginning of year 1 and the end of year 0.
> time point 4 is the beginning of quarter 2 and the end of quarter 1.
> time point 4 is also the beginning of year 2 and the end of year 1.
> time point 8 is the beginning of quarter 3 and the end of quarter 2.
> time point 8 is also the beginning of year 3 and the end of year 2.
> time point 12 is the beginning of quarter 5 and the end of quarter 4.
> time point 12 is also the beginning of year 4 and the end of year 3.
> the remaining balance today is at the end of quarter 12 which is also the end of year 3.
all deposits and withdrawals are made at the end of the quarter shown.
the end of the quarter shown is also the beginning of the next quarter.
for example:
end of quarter 0 is the beginning of quarter 1.
end of quarter 4 is the beginning of quarter 2.
etc.
end of year 0 is also the beginning of year 1.
end of year 1 is also the beginning of year 2.
etc.
the quarterly growth rate factor is equal to (1 + .10/4) = (1 + .025) = 1.025.
your annual growth rate is 10% per year compounded quarterly.
your quarterly growth rate is 10% / 4 = 2.5%.
your effective annual growth rate = 10.3812891% per year.
the effective annual growth rate is calculated as 1.025 ^ 4 = 1.103812891 minus 1 = .103812891 multiplied by 100 = 10.3812891%.
the spreadsheet does not use the effective annual growth rate directly.
it uses the quarterly growth rate factor of 1.025.
the calculating procedure is.
200,000 is deposited at time point 0.
the remaining balance at time 0 is 200,000.
the remaining balance at the next time period is equal to the remaining balance of the previous time period * 1.025 plus any deposits made in that time period.
for example:
in time period 0, the remaining balance is 200,000.
in time period 1, the remaining balance is 200,000 * 1.025 minus 50,000 = 155,000.
in time period 2, the remaining balance is 155,000 * 1.025 minus 50,000 = 108,875.
in time period 2, the remaining balance is 108,875 * 1.0125 minus 0 = 111,596.875.
the spreadsheet shows 111,596.88 because the display is rounded to the nearest penny, but the number stored is 111,596.875.
this procedure continues to the end.
|
|
|