|
Question 118461: solve using cramers rule:
-3x-5y+4z 6000
2x+3y+1z 5000
1x-4y-6z 13000
this is how i solved the question
-3 -5 4 x 6000
2 3 1 y 5000
1 -4 -6 z 13000
-3 3 1 - -5 2 1 + 4 2 3
-4 -6 1 -6 1 -4
-3 (3*-6-1*-4) + 5 (2*-6-1*1) + 4 (2*-4-1*3)
-14 -13 -11
42 -65 -44 -67
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! I can't really tell what you were doing with the determinant evaluation, but I don't think you really have a grasp on the process.
First you need the co-efficient determinant:
 , and in order to evaluate this determinant, you need to augment it by repeating the first two columns.
Now you need the constant matrix, a 3 row X 1 column matrix with the constant values:
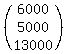
The  determinant is formed by replacing the first column of  with the constant matrix, thus:
 , and augmented,
Cramer's Rule says:
 , so for this problem,  , roughly 7985.
Solving for y and z is the same process, except that you need to calculate the  and  determinants by replacing the second and third columns, respectively, in the coefficient determinant with the constant matrix.
I'll leave you to your arithmetic.
Hope this helps,
John
|
|
|
| |
