|
Question 1184480: Marvin decided to rearrange his stamps in his stamp books, Book A, Book B and Book
C. First, he moved 2/9 of the stamps from Book B to Book C. Then, he moved 3/5 of the
remaining stamps from Book B to Book A. Next, he moved 1/3 of his stamps from Book
A to Book C. In the end, there were 240 fewer stamps in Book B than in Book A. Book
C had 460 more stamps than Book B and there were 600 stamps left in Book C. How
many more stamps were there in Book B than Book A at first?
Found 4 solutions by JBnovelwriter, MathTherapy, ikleyn, 54929:
Answer by JBnovelwriter(34)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Marvin decided to rearrange his stamps in his stamp books, Book A, Book B and Book C. First, he moved 2/9 of the stamps from Book B to Book C. Then, he moved 3/5 of the remaining stamps from Book B to Book A. Next, he moved 1/3 of his stamps from Book A to Book C. In the end, there were 240 fewer stamps in Book B than in Book A. Book C had 460 more stamps than Book B and there were 600 stamps left in Book C. How many more stamps were there in Book B than Book A at first?
The other person is PARTLY-WRONG, but that should be expected seeing that the problem's setup and calculations
are difficult enough to easily make mistakes and end up with one or more INCORRECT answers.
Let number of stamps in Books A, B, and C, be a, b, and c, respectively
After moving  from Book B to Book C, Book B then had from Book B to Book C, Book B then had  left, and Book C had: left, and Book C had:  After moving
After moving  of remainder from Book B to Book A, Book B then had of remainder from Book B to Book A, Book B then had  left.
Book A then had: left.
Book A then had:  After moving
After moving  from Book A to Book C, Book A then had from Book A to Book C, Book A then had  left
Book C then had: left
Book C then had:  As there were 240 fewer stamps in Book B than in Book A, in the end, we get:
As there were 240 fewer stamps in Book B than in Book A, in the end, we get:  2a = 3(240) ------- Cross-multiplying
Original number in Book A, or
2a = 3(240) ------- Cross-multiplying
Original number in Book A, or  As there were 460 more stamps in Book C than in Book B, in the end, we get:
As there were 460 more stamps in Book C than in Book B, in the end, we get: 
 ---- Substituting 600 for ---- Substituting 600 for 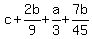 14b = 140(45) ---- Cross-multiplying
Original number in Book B, or
14b = 140(45) ---- Cross-multiplying
Original number in Book B, or  Difference between original number in Book A and Book B:
Difference between original number in Book A and Book B: 
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Marvin decided to rearrange his stamps in his stamp books, Book A, Book B and Book C.
First, he moved 2/9 of the stamps from Book B to Book C.
Then, he moved 3/5 of the remaining stamps from Book B to Book A.
Next, he moved 1/3 of his stamps from Book A to Book C.
In the end, there were 240 fewer stamps in Book B than in Book A.
Book C had 460 more stamps than Book B and there were 600 stamps left in Book C.
How many more stamps were there in Book B than Book A at first?
~~~~~~~~~~~~~~~
Looking into the solutions of the two other tutors, I decided to try the backward method, hoping that the solution will be simpler.
Let's look what I got ( ! )
So, I will accurately divide the entire process by steps.
(1) First, he moved 2/9 of the stamps from Book B to Book C.
(2) Then, he moved 3/5 of the remaining stamps from Book B to Book A.
(3) Next, he moved 1/3 of his stamps from Book A to Book C.
(4) In the end, there were 240 fewer stamps in Book B than in Book A,
and Book C had 460 more stamps than Book B and there were 600 stamps left in Book C.
First of all, based on description of final state (4), we can easily find the number of stamps in each book A, B and C:
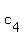 = 600; = 600; 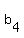 = 600 - 460 = 140; = 600 - 460 = 140;  = 140 + 240 = 380.
Next, I will introduce arrays of numbers = 140 + 240 = 380.
Next, I will introduce arrays of numbers  , ,  , , 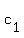 ( distribution of stamps immediately before step 1;
same as the initial distribution of stamps ) ( distribution of stamps immediately before step 1;
same as the initial distribution of stamps )
 , ,  , ,  ( distribution of stamps immediately before step 2) ( distribution of stamps immediately before step 2)
 , , 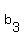 , , 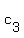 ( distribution of stamps immediately before step 3) ( distribution of stamps immediately before step 3)
 , , 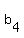 , , 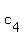 ( distribution of stamps immediately before step 4)
We just found out the values ( distribution of stamps immediately before step 4)
We just found out the values  , , 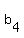 , , 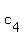 : they are : they are  = 380; = 380; 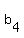 = 140; = 140; 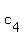 = 600.
We will now move from step (4) to step (3). Marvin's action from step (3) to step (4) was "he moved 1/3 of the stamps from Book A to Book C".
So, we can write = 600.
We will now move from step (4) to step (3). Marvin's action from step (3) to step (4) was "he moved 1/3 of the stamps from Book A to Book C".
So, we can write
 = = 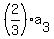 , , 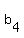 = = 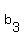 , , 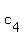 = = 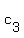 + + 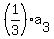 .
First of these equations gives .
First of these equations gives  = = 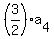 = =  = 570; second gives = 570; second gives 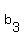 = 140; third gives = 140; third gives 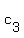 = 600 - = 600 -  = 410.
Thus we can fill the row 3 : = 410.
Thus we can fill the row 3 :  = 570; = 570; 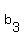 = 140; = 140; 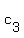 = 410.
We will now move from step (3) to step (2). Marvin's action from step (2) to step (3) was "he moved 3/5 of the stamps from Book B to Book A."
So, we can write = 410.
We will now move from step (3) to step (2). Marvin's action from step (2) to step (3) was "he moved 3/5 of the stamps from Book B to Book A."
So, we can write
 = = 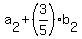 , , 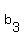 = = 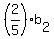 , , 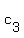 = =  .
First of these equations gives 570 = .
First of these equations gives 570 = 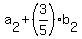 ; second gives 140 = ; second gives 140 = 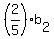 ; third gives ; third gives  = 410.
It implies = 410.
It implies  = = 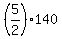 = 350; 570 = = 350; 570 = 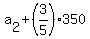 = =  + 210; hence, + 210; hence,  = 570-210 = 360.
Thus we can fill the row 2 : = 570-210 = 360.
Thus we can fill the row 2 :  = 360; = 360;  = 350; = 350;  = 410.
We will now move from step (2) to step (1). Marvin's action from step (1) to step (2) was "he moved 2/9 of the stamps from Book B to Book C."
So, we can write = 410.
We will now move from step (2) to step (1). Marvin's action from step (1) to step (2) was "he moved 2/9 of the stamps from Book B to Book C."
So, we can write
 = =  , ,  = = 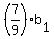 , ,  = = 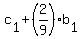 .
First of these equations gives .
First of these equations gives  = 360; second gives = 360; second gives  = = 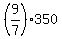 = 450; third gives = 450; third gives 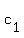 = = 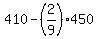 = 310.
Thus we can fill the row 1 : = 310.
Thus we can fill the row 1 :  = 360; = 360;  = 450; = 450; 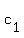 = 310.
So the answer to the problem question is = 310.
So the answer to the problem question is  - -  = 450-360 = 90 stamps. ANSWER = 450-360 = 90 stamps. ANSWER
Solved.
After obtaining this ANSWER, I, naturally, checked it, walking through the steps from (1) to (4).
What I got, confirmed correctness of my calculations.
Answer by 54929(12)   (Show Source): (Show Source):
|
|
|
| |