|
Question 1184444: Ali, Ben, Cain and Dan, shared a sum of money.
Ali has 1/2 of the total amount of money that Ben, Cain and Dan have.
Ben has 1/3 of the total amount of money that Ali, Cain and Dan have.
Cain has 1/7 of the total amount of money that Ali, Ben and Dan have.
(a) What fraction of the total sum of money does Dan have?
(b) Dan has $84. Find the sum of money shared by the 4 boys.
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(a) Ali has 1/2 of the total amount of money that Ben, Cain and Dan have.
Let x be the amount Ali has; then 2x is the total amount the other three have.
The total amount all of them have is then 3x.
That means Ali has 1/3 of the total they all have.
Similarly, Ben having 1/3 of the total that the other three have means Ben has 1/4 of the total amount.
And similarly Cain has 1/8 of the total amount.
Together, the fraction of the total amount that Ali, Ben, and Cain have is
1/3+1/4+1/8 = 8/24+6/24+3/24 = 17/24; that means Dan has 7/24 of the total amount.
ANSWER: Dan has 7/24 of the total amount.
(b) Dan's $84 is 7/24 of the total:


ANSWER: The total amount the four boys had was $288.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Greenestamps did it the most elementary way. Think I'll do it using
matrices. Maybe you've gotten that far.
>>>Ali, Ben, Cain and Dan, shared a sum of money.
>>>Let A,B.C.D be the fractions of their shares. Then the sum of the
four fractions must be 1 (whole).
So 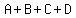   >>>Ali has 1/2 of the total amount of money that Ben, Cain and Dan have.
>>>Ali has 1/2 of the total amount of money that Ben, Cain and Dan have.
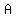  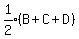 >>>Ben has 1/3 of the total amount of money that Ali, Cain and Dan have.
>>>Ben has 1/3 of the total amount of money that Ali, Cain and Dan have.
  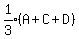 >>>Cain has 1/7 of the total amount of money that Ali, Ben and Dan have.
>>>Cain has 1/7 of the total amount of money that Ali, Ben and Dan have.
  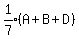 The system is
The system is
     The matrix is
The matrix is
 Do row operations on that to get the row reduced echelon form (RREF)
of the matrix above. Your TI-84 can handle that if you understand the
matrix feature.
The RREF matrix form of that is as below
Do row operations on that to get the row reduced echelon form (RREF)
of the matrix above. Your TI-84 can handle that if you understand the
matrix feature.
The RREF matrix form of that is as below
 So Ali got 1/3, Ben got 1/4, Cain got 1/8, and Dan got 1/7.
------------------------------------
For (b)
Let $S = the total amount,
Then Dan's share was 7/24 of $S
So
So Ali got 1/3, Ben got 1/4, Cain got 1/8, and Dan got 1/7.
------------------------------------
For (b)
Let $S = the total amount,
Then Dan's share was 7/24 of $S
So 

 [Greenestamps was right!]]
Ali got 1/3 of $288 or $96
Ben got 1/4 of $288 or $72
Cain got 1/8 of $588 or $36
Dan got $84
Check:
The sum was $96
$72
$36
$84
---
$288 as we expected.
Edwin
[Greenestamps was right!]]
Ali got 1/3 of $288 or $96
Ben got 1/4 of $288 or $72
Cain got 1/8 of $588 or $36
Dan got $84
Check:
The sum was $96
$72
$36
$84
---
$288 as we expected.
Edwin
|
|
|
| |