Question 1184399: If a, b, c, p, q, r are positive real numbers such that a, b, c are in the geometric sequence and the condition  is satisfied then which of the following is true:
A- p, q, r are in Geometric Sequence
B- p, q, r are in Arithmetic Sequence
C- p, q, r are in Harmonic Sequence
D- p^2, q^2, r^2 are in Geometric Sequence
E- p^2, q^2, r^2 are in Arithmetic Sequence
...
[NOTE: Here ^2 means power 2]
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!
To find out which choice(s) is(are) feasible, let's look at a specific
example:
a = 2, b = 4, c = 8, p = 6, q = 3, r = 2
(a,b,c) = (2,4,8) are in geometric sequence
is satisfied because
(p,q,r) = (6,3,2) are not in geometric nor arithmetic sequence.
(p,q,r) = (6,3,2) are in harmonic sequence because their
reciprocals (1/6, 1/3, 1/2) are (1/6,2/6,3/6) are in arithmetic
sequence.
(p2,q2,r2) = (62,32,22) = (36,9,4) are not in geometric nor in arithmetic sequence.
This is a counter-example to all choices but C. So, A,B,D,E are disproved.
So if we are given that one of the choices is correct, then that correct
choice can only be C. But it is possible that "none of these" is the
answer, although it is not listed.
So we must prove that if (a,b,c) are in geometric sequence, and
then (p,q,r) are in harmonic sequence, which means
that
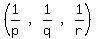is in arithmetic sequence. But as yet I have not proved it. Maybe Ikleyn or
greenestamps can help. I'll keep working on it.
Edwin
|
|
|
