|
Question 1184395: Eric and Patrick were playing a card game. In the first round, Eric lost 1/3 of his cards to Patrick.
In the second round, Patrick lost 0.25 of the cards he had then to Eric. In the last round, Eric
lost 1/5 of his cards he had then to Patrick. In the end, Eric had 760 cards and Patrick had 1324 cards. How many cards did Eric have at first?
Found 3 solutions by Theo, MathTherapy, 54929:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i spent a lot of time going through this and then the computer went and lost all my work.
i don't have time to repeat the whole procedure now, so i'll just give you the solution.
in the beginning, eric had 858 and patrick has 1226 = 2084 total cards.
in the end, eric had 760 + 1324 = 2084 total cards.
confirming the number of cards is correct, i went from the beginning to the end.
in the beginning, eric had 858 cards and patrick had 1226.
in the first round, eric lost 1/3 of his cards to patrick.
eric now had 858 - 1/3 * 858 = 572 and patrick now had 1226 + 1/3 * 858 = 1512.
in the second round, patrick lost 1/4 of his cards to eric.
eric now had 572 + 1/4 * 1512 = 950 and patrick now had 1512 - 1/4 * 1512 = 1134.
in the final round, eric lost 1/5 of his cards to patrick.
eric now had 950 - 1/5 * 950 = 760 and patrick had 1134 + 1/5 * 950 = 1324.
number look good.
in the beginning, eric had 858 cards and patrick had 1226 = 2084 total cards for both.
in the end, eric had 760 + 1324 = 2084 total cards for both.
your solution should be that eric had 858 cards at first.
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Eric and Patrick were playing a card game. In the first round, Eric lost 1/3 of his cards to Patrick.
In the second round, Patrick lost 0.25 of the cards he had then to Eric. In the last round, Eric
lost 1/5 of his cards he had then to Patrick. In the end, Eric had 760 cards and Patrick had 1324 cards. How many cards did Eric have at first?
Let original number of cards Eric and Patrick had, be E and P, respectively
After losing  of his cards to Patrick, Eric was left with of his cards to Patrick, Eric was left with 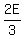 , and Patrick had: , and Patrick had: 
After losing ¼ of his cards to Eric, Patrick was left with ¾ * 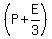 , or , or  , and Eric then had: , and Eric then had: 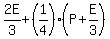 , or , or  , or , or 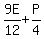 , or , or 
After losing  of his cards to Patrick, Eric was left with of his cards to Patrick, Eric was left with  , or , or 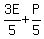 , and Patrick had: , and Patrick had: 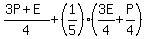 , or , or 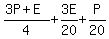
In the end, we have for Eric and Patrick, the following:
 
P + 3E = 3,800______P = 3,800 - 3E ------- eq (i)
16P + 8E = 26,480 ------ eq (ii)
16(3,800 - 3E) + 8E = 26,480 ------ Substituting 3,800 - 3E for P in eq (ii)
60,800 - 48E + 8E = 26,480
- 48E + 8E = 26,480 - 60,800
- 40E = - 34,320
Original number of cards Eric had, or 
You could've approached it from the END, instead of the beginning. This would've been less complex and probably less time-consuming.
Maybe you can start at the end and see if you come up with Eric's original count of 858 cards.
Answer by 54929(12)   (Show Source): (Show Source):
|
|
|
| |