Question 118436: A rectangular box is to be placed in the first quadrant in such a way that one side lies on the positive x-axis and one side lies on the positive y-axis. The box is to lie below the line y=-2x+5. Give the dimensions of such a box having greatest possible area.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
given:

known: positions for the rectangular box defined by the  and and  minimums and maximums minimums and maximums
so, to find out what the dimensions of such a box are, first find midpoint coordinates of the line segment between  and and 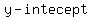 or or
between points
 , , = =  , , and and
 , , = =  , ,
That will be:
 coordinate of mid point is coordinate of mid point is 
 coordinate of mid point is coordinate of mid point is 
The mid point of segment joining two point is:
(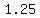 , , ) )
Here is the graph that shows the point (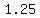 , , ): ):
| Solved by pluggable solver: FIND EQUATION of straight line given 2 points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (1.25, 2.5) and (x2, y2) = (0, 5).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(-2)x + (5)
Your graph:

|
the dimensions of a box are:  and and 
its greatest possible area is:



|
|
|