.
The foci of the ellipse 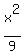 +
+  = 1 are the points (-c,0) and (c,0) on x-axis, where c =
= 1 are the points (-c,0) and (c,0) on x-axis, where c = 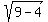 =
=  .
The locus of points P such that the foci subtend the right angle at point P is the circle,
centered at the origin of the coordinate plane and having the radius of
.
The locus of points P such that the foci subtend the right angle at point P is the circle,
centered at the origin of the coordinate plane and having the radius of  , EXCLUDING
the endpoints of its diameter that lie on x-axis.
, EXCLUDING
the endpoints of its diameter that lie on x-axis.
Solved, answered and explained.