SOLUTION: If four distinct points (2k, 3k), (2, 0), (0, 3) and (0, 0) lie on circle then which condition is true from the following: A- k < 0 B- 0 < k < 1 C- k = 1 D- k > 1

Straight line segment connecting the points (2,0) and (0,0) is horizontal  y= 0;

    hence, the center of the circle lies at the perpendicular bisector x = 1.



Straight line segment connecting the points (0,3) and (0,0) is vertical  x= 0;

    hence, the center of the circle lies at the perpendicular bisector y = 1.5.



        It implies that the center of the circle is the point  (1,1.5).



Thus we see, that three points  (0,0) (at the circle),  (1.1.5) (the circle center)  and  (2k,3k) (at the circle)  all lie 

on the same straight line  y = 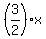  (the circle's diameter).



It may happen if and only if  k = 0  or  k = 1.



The case  k = 0  leads to the existing point (0,0).  

Since from the context, the point (2k,3k) is distinct from (0,0), it leaves only one remaining possibility for k to be equal to 1:  k = 1.



ANSWER.  The only option is  C :  k = 1.