Question 118426: An open box is to be made from a 10 cm by 20 cm rectangular piece of cardboard by cutting a square from each corner and folding up the sides. The area of the bottom of the box is 96 cm squared. What is the length of the sides of the squares that are cut from the corners?
I really need help solving this algebraically. If you could help that would be amazing!
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you draw a picture, you can see that the dimensions of the bottom of the box are 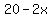 by by 

So the area of the bottom is 
 Now plug in the given area Now plug in the given area 
 Foil Foil
 Subtract 96 from both sides Subtract 96 from both sides
 Combine like terms Combine like terms
 Rearrange the terms Rearrange the terms
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=4, b=-60, and c=104 Plug in a=4, b=-60, and c=104
 Negate -60 to get 60 Negate -60 to get 60
 Square -60 to get 3600 (note: remember when you square -60, you must square the negative as well. This is because Square -60 to get 3600 (note: remember when you square -60, you must square the negative as well. This is because  .) .)
 Multiply Multiply 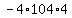 to get to get 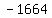
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 4 to get 8 Multiply 2 and 4 to get 8
So now the expression breaks down into two parts
 or or 
Lets look at the first part:

 Add the terms in the numerator Add the terms in the numerator
 Divide Divide
So one answer is

Now lets look at the second part:

 Subtract the terms in the numerator Subtract the terms in the numerator
 Divide Divide
So another answer is

So our possible solutions are:
 or or 
However, since 13 is greater than 10, the solution  is not possible since the square cutout cannot have a longer length than one of the sides. is not possible since the square cutout cannot have a longer length than one of the sides.
So our only solution is 
------------
Check:
Remember, the area is

 Plug in the given area Plug in the given area  and and 
 Multiply Multiply
 Subtract Subtract
 Multiply. Since the two sides of the equation are equal, this verifies our answer. Multiply. Since the two sides of the equation are equal, this verifies our answer.
|
|
|