Question 1184224: The coefficients of the powers of x in the 2nd, 3rd and 4th term of the expansion  is in arithmetic progression where n is positive integer. Find the number of coefficients of the odd powers of x in the expansion?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52818)   (Show Source):
You can put this solution on YOUR website! .
A quick solution is as follows.
Look at the Pascal's triangle in this Wikipedia article
https://en.wikipedia.org/wiki/Pascal%27s_triangle
You will see momentarily that the sought line is the 8th line for  .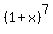
Those coefficients are 7, 21, 35.
The sum of coefficients at odd degrees is HALF of the total sum, which is  = 128.
THEREFORE, the answer to the problem's question is 128/2 = 64.
Solved.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
The coefficients that are in arithmetic progression can be found algebraically; however, it is unclear what the question is asking for....
The coefficients in the expansion of (1+x)^n are...
1st term: 
2nd term: 
3rd term: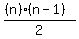 
4th term: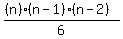 
The 2nd, 3rd, and 4th terms are in arithmetic progression, so the 3rd term is twice the sum of the 2nd and 4th terms:
n=7 or n=2
n=2 makes no sense in the problem because (1+x)^2 only has 3 terms.
So n=7.
The 2nd, 3rd, and 4th terms in the expansion of (1+x)^7 are 7, 21, and 35 -- in arithmetic progression with common difference 14.
But I don't know how to answer the question because I don't know what it means:
"Find the number of coefficients of the odd powers of x in the expansion."
The expansion of (1+x)^7 has 8 terms; half of them are even powers of x and half are odd powers.
So I guess the answer is 4.
But after doing some good math to find a value of n for which the coefficients of the 2nd, 3rd, and 4th terms in the expansion of (1+x)^n form an arithmetic progression, that seems like a very odd question to ask....
|
|
|
