SOLUTION: If {{{ (z-1)/(z+1) }}} is purely imaginary then what is value of |z|?

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: If {{{ (z-1)/(z+1) }}} is purely imaginary then what is value of |z|?      Log On


   

Question 1184217: If 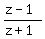+%28z-1%29%2F%28z%2B1%29+ is purely imaginary then what is value of |z|?
Found 2 solutions by robertb, ikleyn:
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
If +%28z-1%29%2F%28z%2B1%29+ is purely imaginary, then +%28z-1%29%2F%28z%2B1%29+=+Ai for some A%3C%3E0.
Let z = a + bi.
===> z - 1 = A(z+1)i ===> a + bi - 1 = A(a + bi + 1)i
===> a + bi - 1 = A((a + 1)i - b) = A(a+1)i - Ab

<===> (a - 1 + Ab) + (b - A(a+1))i = 0
===> a - 1 + Ab = 0 and b - A(a+1) = 0, or
===> a + Ab = 1 and -Aa + b = A.
===> a+=+%281-A%5E2%29%2F%281%2BA%5E2%29 and b+=+%282A%29%2F%281%2BA%5E2%29 after solving the system for a and b.
===> z++=+a%2Bbi+=++%281-A%5E2%29%2F%281%2BA%5E2%29+%2B+i%2A%28%282A%29%2F%281%2BA%5E2%29%29
===>

=

Therefore, highlight%28abs%28z%29+=+1%29


Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.


            This problem has a nice geometric interpretation. 


1 and -1 are selected points in the complex number plane.


For an arbitrary complex number z, the numbers z-1 and z+1 are vectors, connecting z with the points 1 and -1.



The condition that 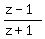 %28z-1%29%2F%28z%2B1%29  is purely imaginary means that the vectors z-1 and z+1 are perpendicular.



So, the problem asks to find points z in complex plane, such that the "visibility angle" from z to 

these points "1" and "-1" is the right angle.


Or, in other terms, find points z in complex plane, such that the angle between the vectors z-1 and z+1 is the right angle.



Clearly, these points are on the unit circle, and they provide the right angle leaning on the segment [-1,1]

as on the diameter of the unit circle.   So, |z| = 1.    ANSWER