|
Question 1184210: Find the locus of point if point moves in such way that the difference of its distance from two points (8, 0) and (-8, 0) always remains 4?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the locus of point if point moves in such way that the difference of its distance from two points (8, 0) and (-8, 0) always remains 4?
~~~~~~~~~~~~~~~~~
If the difference of distances of the point from two given points is a constant, then (it is a known fact) the locus is a HYPERBOLA.
The problem is to write an equation if this hyperbola.
There are two ways to do it.
One way is long and tortured: it is to write literally what is given
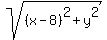 - - 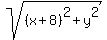 = 4,
then to isolate square roots and square both sides;
then to isolate square root again and square both sides AGAIN;
then simplify, and at the end you will get the sought equation.
For the general case, this way is shown in many standard textbooks.
You can read it from the lesson
- Hyperbola focal property
in this site.
Another way is shorter; but it assumes that you just have some preliminaries knowledge on the subject.
So, the focuses of the hyperbola are (-8,0) and (8,0); thus the transverse axis is x-axis and the hyperbola is centered at (0,0);
one vertex is (x,0), the other vertex is (-x,0);
for the vertex (x,0) the difference of distances from the focuses gives this equation
(8-x) - (x-(-8)) = 4 ====> 8-x - (x+8) = 4 ====> 8 - x - x - 8 = 4 ====> -2x = 4 ====> x = -2.
So, the vertices are (-2,0) and (2,0).
Thus the transverse semi-axis is a = = 4,
then to isolate square roots and square both sides;
then to isolate square root again and square both sides AGAIN;
then simplify, and at the end you will get the sought equation.
For the general case, this way is shown in many standard textbooks.
You can read it from the lesson
- Hyperbola focal property
in this site.
Another way is shorter; but it assumes that you just have some preliminaries knowledge on the subject.
So, the focuses of the hyperbola are (-8,0) and (8,0); thus the transverse axis is x-axis and the hyperbola is centered at (0,0);
one vertex is (x,0), the other vertex is (-x,0);
for the vertex (x,0) the difference of distances from the focuses gives this equation
(8-x) - (x-(-8)) = 4 ====> 8-x - (x+8) = 4 ====> 8 - x - x - 8 = 4 ====> -2x = 4 ====> x = -2.
So, the vertices are (-2,0) and (2,0).
Thus the transverse semi-axis is a = 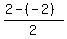 = 2 units long,
and for the imaginary semi-axis "b" we have = 2 units long,
and for the imaginary semi-axis "b" we have  + +  = =  , where c = 8 is half the distance between the focuses;
so , where c = 8 is half the distance between the focuses;
so 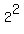 + +  = =  , or , or  = 64 - 4 = 60, b = = 64 - 4 = 60, b = 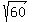 .
Thus the canonic equation of the hyperbola is .
Thus the canonic equation of the hyperbola is
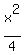 - - 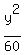 = 1. = 1.
Solved.
--------------
For the preliminaries knowledge on hyperbolas, see the lessons
- Hyperbola definition, canonical equation, characteristic points and elements
- Hyperbola focal property
- Tangent lines and normal vectors to a hyperbola
- Optical property of a hyperbola.
in this site.
|
|
|
| |