Question 1184181: In a group of 140 tourists it was found that 88 had visited Britain, 90 had visited Australia, 76 had visited New Zealand, 48 had visited both Britain and Australia, 43 had visited both Britain and New Zealand, 50 had visited both New Zealand and Australia, while 19 had visited all three countries.
i) Draw a Vann diagram to illustrate the information above.
ii) A tourist is chosen at random from this group, find the probability that the chosen tourist visited Australia and exactly one other country.
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a group of 140 tourists it was found that 88 had visited Britain, 90 had visited Australia,
76 had visited New Zealand, 48 had visited both Britain and Australia, 43 had visited
both Britain and New Zealand, 50 had visited both New Zealand and Australia, while 19 had visited all three countries.
i) Draw a Vann diagram to illustrate the information above.
ii) A tourist is chosen at random from this group, find the probability that the chosen tourist visited Australia and exactly one other country.
~~~~~~~~~~~~~~~~~~~~~~~
The set of tourists, who visited Australia and exactly one other country
is equal to the set of tourists who visited Australia MINUS the subset of those
who visited all three countries.
Therefore, the answer to the problem's question is
P = 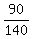 - - 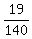 = = 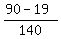 = = 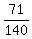 . .
Solved, answered and explained.
|
|
|