SOLUTION: If p, q and r are the sides opposite to the angles P, Q and R respectively in a triangle PQR. If {{{ r^2SinPSinQ = pq}}} then the triangle PQR is: (a) Equilateral (b) Acute Angle

Algebra ->  Trigonometry-basics -> SOLUTION: If p, q and r are the sides opposite to the angles P, Q and R respectively in a triangle PQR. If {{{ r^2SinPSinQ = pq}}} then the triangle PQR is: (a) Equilateral (b) Acute Angle      Log On


   

Question 1184169: If p, q and r are the sides opposite to the angles P, Q and R respectively in a triangle PQR. If +r%5E2SinPSinQ+=+pq then the triangle PQR is:
(a) Equilateral
(b) Acute Angle but not equilateral
(c) Obtuse Angle
(d) Right Angle
(e) Right Angle as well as Isosceles
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

It is very well known fact from Geometry that for any triangle PQR with the sides p, q, r opposite to angle P,Q, R respectively,


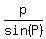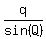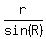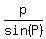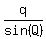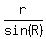the ratios  p%2Fsin%28P%29,  q%2Fsin%28Q%29,  r%2Fsin%28R%29  are all equal and are equal to the diameter of the circle circumscribed around the triangle PQR


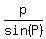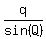     p%2Fsin%28P%29 = q%2Fsin%28Q%29 = r%2Fsin%28R%29 = d.



For the proof see, for example, lesson

    - Law of sines - the Geometric Proof 

in this site.



Then from the given part of the problem, we see that


    r%5E2 = p%2Fsin%28P%29.q%2Fsin%28Q%29 = d*d = d^2.


In other words, the square of the side "r"  is equal to the square of the diameter of circumscribed circle


             r%5E2 = d%5E2.



It implies  r = d,  i.e.  the side "r"  is the diameter of the circumscribed circle about triangle PQR.


It means that the angle R is leaning on the diameter of the circumscribed circle,

i.e. triangle PQR is a right-angled triangle with the right angle at vertex R.


So, the given triangle is a right-angled triangle.


ANSWER.  PQR is a right-angled triangle.

Solved.