SOLUTION: {{{If arcSin(x) + arcSin(y) + arcSin(z)}}} = 3pi/2}}} then find value of x^9 + y^9 + z^9 - (1/x.y.z)^9 where / means division and ^9 means power 9.

Algebra ->  Trigonometry-basics -> SOLUTION: {{{If arcSin(x) + arcSin(y) + arcSin(z)}}} = 3pi/2}}} then find value of x^9 + y^9 + z^9 - (1/x.y.z)^9 where / means division and ^9 means power 9.      Log On


   

Question 1184167: If+arcSin%28x%29+%2B+arcSin%28y%29+%2B+arcSin%28z%29 = 3pi/2}}} then find value of x^9 + y^9 + z^9 - (1/x.y.z)^9 where / means division and ^9 means power 9.
Answer by ikleyn(52810) About Me  (Show Source):
You can put this solution on YOUR website!
.
If arcsin(x) + arcsin(y) + arcsin(z) = 3pi%2F2 then find value of x^9 + y^9 + z^9 - (1/x.y.z)^9 where / means division and ^9 means power 9.
~~~~~~~~~~~~~~~~~~~~~~~~ 

Function  arcsin()  has the range from  -pi%2F2  to  pi%2F2.


Therefore, if  arcsin(x) + arcsin(y) + arcsin(z) = 3pi%2F2,  then it implies

    arcsin(x) = arcsin(y) = arcsin(z) = pi%2F2.


Hence,

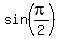    x = y = z = sin%28pi%2F2%29 = 1.


Therefore,

    x^9 + y^9 + z^9 - 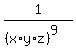1%2F%28%28x%2Ay%2Az%29%5E9%29 = 1 + 1 + 1 - 1 = 2.


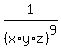ANSWER.  If  arcsin(x) + arcsin(y) + arcsin(z) = 3pi%2F2  then  x^9 + y^9 + z^9 - 1%2F%28x%2Ay%2Az%29%5E9 = 2.

Solved.