Question 1184112: Solve the inequality in terms of intervals and illustrate the solution set on the real number line.
x^3 > x
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
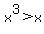
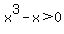
A graph will help us check our answer....
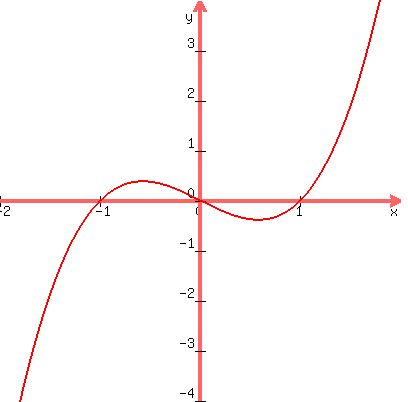
The graph shows the function is greater then 0 between -1 and 0, and for x greater than 1. So our answer should be (-1,0) U (1,infinity).
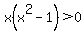
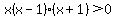
The function is equal to 0 at -1, 0, and 1; those x values divide the x axis into 4 intervals. A standard method for finding the answer is to pick a point in each interval and see whether the function value there is positive.
I'll let you do that if you want, or if that is how you have been taught and you are required to get the final answer that way.
For a simplification of the process, simply pick one point anywhere, determine whether the function value is positive or negative, and then "walk" along the number line, seeing what happens to the sign of the function when you pass each of the zeros.
The function again is

I find it easiest to pick a "large" number first -- that is, greater than the largest zero.
If x>1, then all three factors in the factored form of the function are positive, so the inequality is satisfied for all x>1.
Now I "walk" along the x-axis to the left....
when I pass x=1, one factor changes sign, so the sign of the function changes; so just to the left of x=1 the function value is negative.
when I pass x=0, another factor changes sign, so the function value becomes positive again.
and when I pass x=-1, the third factor changes sign, and the function value is again negative.
So the function value is positive, and the inequality is satisfied, when x>1 and between x=0 and x=-1.
ANSWER: (-1,0) U (1,infinity) -- which agrees with what we saw from the graph.
|
|
|