|
Question 1184054: Ken had 1 1/2 times as many bookmarks as Lionel. Mike had 3/4 as many bookmarks as
Ken. Ken and Lionel gave Mike a number of bookmarks in the ratio 3:1. As a result, Mike
had twice as many bookmarks as before, and Lionel had 32 bookmarks more than Ken.
How many bookmarks did Ken give to Mike?
Found 6 solutions by 54929, Octo-pie7, papachick24025, greenestamps, josgarithmetic, MathTherapy:
Answer by 54929(12)   (Show Source):
You can put this solution on YOUR website! To calculate the number of bookmarks that Ken gave to Mike.
Let consider x to be the number of Lionel's bookmark. According to question, we have
Bookmarks of Ken = 1 1/2 * Bookmarks of Lionel
Bookmarks of Ken = 1.5x
Bookmarks of Mike = (3/4) * Bookmarks of Ken
Bookmarks of Mike = (3/4) * (1.5x)
Bookmarks of Mike = 1.125x
If Ken give 3y bookmarks to Mike then Lionel gives 1y bookmarks to Mike. The total number of bookmarks each of one have now is given by,
Bookmarks of Ken = 1.5x - 3y
Bookmarks of Mike = 1.125x + 4y
Bookmarks of Lionel = x - y
Bookmarks of Mike now = 2(Previous bookmarks of Mike)
⇒ 1.125x + 4y = 2(1.125x)
Bookmarks of Lionel = Bookmarks of Ken + 32
⇒ x - y = 1.5x - 3y + 32
On solving both the equations, we get
x = 512
y = 144
Thus, the Ken gave 3(144) =
432
bookmarks to the Mike.
Answer by Octo-pie7(11)  (Show Source):
You can put this solution on YOUR website! Let Lionel has x bookmarks
Therefore Ken had 1 1/2x = 3/2x bookmarks.
And Mike had 3/4 * 3/2x = 9/8x bookmarks.
Ken and Lionel gave Mike a number of
bookmarks in the ratio 3:1
Let Lionel gave y bookmarks then Ken gave
3y bookmarks
Now, Ken has = 3/2x-3y bookmarks
Lionel has = x-y bookmarks
Mike had = 9/8x + 4y
As a result Mike had twice as many
bookmarks as before
So, 9/8x + 4y = 2 * 9/8x
=> 9x = 32y ———— 1
Lionel had 32 bookmarks more than
Ken.
Therefore x-y = 3/2x x 3y + 32.
=> x + 64 = 4y ———— 2
Solving 1 & 2,
x = 64 * 8 = 512
y = 144.
Then Ken gave bookmarks to Mike = 3y
= 3 * 144 = 432
Answer by papachick24025(6)  (Show Source):
You can put this solution on YOUR website! From the first sentence of the problem, we know that:
K = (3/2)L
From the second sentence of the problem, we know that:
M = (3/4)K
From the third sentence of the problem, we know that:
k gave m 3x bookmarks and l gave m x bookmarks. Therefore,
M + 4x = 2(M)
Simplifying this equation gives us:
M = 4x
We also know from the last sentence of the problem that:
L = K + 32
Now we can substitute our expressions for K and M in terms of L into our equation for M:
(3/4)(3/2)L + 4x = 8x
Simplifying this equation gives us:
9L/8 + 4x = 8x
9L/8 = 4x
L = (32/9)x
Substituting this expression for L into our equation for K gives us:
K = (3/2)(32/9)x = (16/3)x
Finally, we can substitute our expressions for K and M in terms of x into our equation for M:
M = (3/4)(16/3)x = 4x
Therefore, k gave m 3x bookmarks, and since m ended up with 4x bookmarks in total, we have:
3x + x = 4x
Solving for x gives us:
x = 144
Therefore, k gave m 3x = 432 bookmarks.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The solution from the other (new) tutor is fine.... But it involves a lot of computations with "ugly" fractions.
Since there are many different paths to the solution to the problem, let's try something different and see if we find an easier path to the solution.
When the statement of the problem gives ratios, it is often easiest to set up the problem using those ratios.
In this problem, we have...
(1) K:L = 3:2
(2) M:K = 3:4
We can use a single variable to solve the problem by finding the ratio M:K:L. Do that by multiplying each of the given ratios by a constant so that the "K" in both ratios is the same number.
(1) K:L = 3:2 = 12:8
(2) M:K = 3:4 = 9:12
(3) M:K:L = 9:12:8
Having done that manipulation with the given ratios...
Let 9x = number Mike starts with
Let 12x = number Ken starts with
Let 8x = number Lionel starts with
Mike ends up with twice as many as he had to start, so
18x = number Mike ends with
Between them, the number Ken and Lionel gave Mike was 9x. Ken gave Mike 3 times as many as Lionel gave, so Ken gave Mike 3/4 of the 9x and Lionel gave Mike 1/4 of the 9x:
(3/4)9x = (27/4)x = number Ken gave Mike
(1/4)9x = (9/4)x = number Lionel gave Mike
Then...
the number Ken ends up with is 12x-(27/4)x = (21/4)x
the number Lionel ends up with is 8x-(9/4)x = (23/4)x
Lionel ends up with 32 more than Ken:
(23/4)x-(21/4)x = 32
(2/4)x = (1/2)x = 32
x = 64
We could figure out all the numbers in the problem -- the numbers each of them started with and the numbers each of them ended with. But the problem only asks for the number Ken gave to Mike. That number is
(27/4)x = (27/4)(64) = 27*16 = 432
ANSWER: 432
If this forum works the way it is supposed to, you will get another response or two showing still different ways to set up and solve the problem.
Answer by josgarithmetic(39617) (Show Source):
You can put this solution on YOUR website!
INITIAL GAVE 3:1, 3r:r
Ken (3/2)x (3/2)x-3r
Lionel x x-r
Mike (3/4)(3/2)x=(9/8)x (9/8)x+4r
-------------------------------------
As a result, Mike
had twice as many bookmarks as before, and Lionel had 32 bookmarks more than Ken.
How many bookmarks did Ken give to Mike?
-------------------------------------
.
.
.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Ken had 1 1/2 times as many bookmarks as Lionel. Mike had 3/4 as many bookmarks as
Ken. Ken and Lionel gave Mike a number of bookmarks in the ratio 3:1. As a result, Mike
had twice as many bookmarks as before, and Lionel had 32 bookmarks more than Ken.
How many bookmarks did Ken give to Mike?
Let original number Lionel had, be L
Then original number Ken had was, 1.5L
Also, Mike’s original number = 
Since Ken and Lionel gave Mike an amount in a ratio of 3:1, then Ken and Lionel gave Mike 3x, and x, respectively,
with x being the MULTIPLICATIVE factor of the total number given to Mike. In all, Mike received 4x (3x + x) from
Ken and Lionel
After Ken gave Mike 3x, Ken was left with 1.5L - 3x
After Lionel gave Mike x, Lionel was left with L - x
After receiving a total of 4x from Ken and Lionel, Mike then had: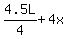 
After receiving 4x from Ken and Lionel, Mike had twice his previous total,
so we get: 
2(4.5L) - 4.5L = 4(4x) ------ Multiplying by LCD, 4
4.5L = 16x
4.5L - 16x = 0 ------- eq (i)
Now, since Ken was left with 32 LESS than Lionel, after giving to Mike, we then have:
1.5L - 3x = L - x - 32
1.5L - L - 3x + x = - 32
.5L - 2x = - 32 ----- eq (ii)
4.5L - 18x = - 288 ---- Multiplying eq (ii) by 9 --- eq (iii)
2x = 288 ------ Subtracting eq (iii) from eq (i)
Multiplicative factor of number given to Mike, or 
Ken gave Mike, 3x = 3(144) = 432
|
|
|
| |
