SOLUTION: prove by mathematical induction: 1^5 + 2^5 + 3^5 + ... + n^5 = (1/12)n^2(n+1)^2(2n^2 + 2n -1)

Base case:   = 1

             =  = 1



Base case holds.





Hypothesis:  

Assume  + ... +  =  for n=k.  (*)





Step case:  Let n=k+1

 [  + ... +  ] +  



... use hypothesis on terms within [  ] ...



=  + 



... this reduces to (you can factor  then use a factoring website for the rest) ...  (see NOTE)



= 



The proof is complete here, but it is not obvious, so

let u=k+1 --> k=u-1



= 

= 



Proof complete



NOTE:  I admit, there may be an easier path here.  If other tutors (or the student) wish to find it, more power to them.  I gave the general idea...



If this helps the student, thanks are appreciated.  

    

(a) The base of induction: n = 1.

    Then the sum is one single term 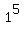 ,  which is 1.

    The formula (*) at n = 1 gives 

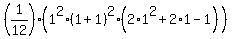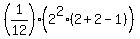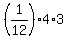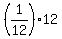         =  =  =  = 1,  

    so the base of induction is established.



(b)  The step of induction.

     We assume that for some integer k >= 1 this formula is valid

         1^5 + 2^5 + 3^5 + . . . + k^5 = 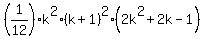.     (1)


     We want to prove that then the formula is valid for the next integer number k+1, too:

         1^5 + 2^5 + 3^5 + . . . + k^5 + (k+1)^5 = .     (2)


     At this point, the proof of the formula (2) is started.


     In the left side of (2), we replace the sum of the first k addends by the right side expression (1).

     Thus we want to prove

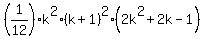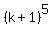          +  = .     (3)


     Let's transform left side of (3). We factor it, taking the common factor 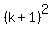 out of parentheses.

     Then left side of (3) takes the form

            = 

         =  = 

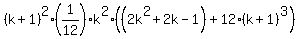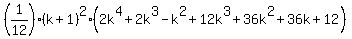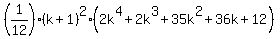         = .    (4)

    
     Now, I used an online calculator to factor an expression in the internal parentheses,
     and the calculator produced this decomposition

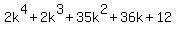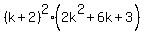          = .     (5)

     ( the link to the calculator is  https://www.pocketmath.net , the mode is "Factor" )  )


     This factorization can be continued this way
     
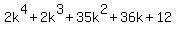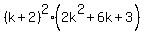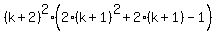          =  = .    (6)


     Now, combining all pieces (4), (5) and (6) in one whole block, we have

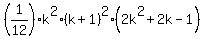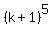          +  = .   (7)


     It is the same as (identical to) formula (3).  Thus formula (3) is proven.



(3)  Due to the principle of the mathematical induction, it means that formula 

          = .     

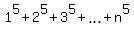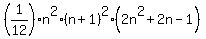     is proved for all integer n >= 1.