SOLUTION: prove by mathematical induction: 1^5 + 2^5 + 3^5 + ... + n^5 = (1/12)n^2(n+1)^2(2n^2 + 2n -1)

Base case: 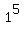  = 1

             =  = 1



Base case holds.





Hypothesis:  

Assume 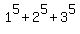 + ... +  =  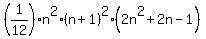for n=k.  (*)





Step case:  Let n=k+1

 [  + ... +  ] +  



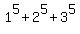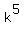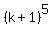
... use hypothesis on terms within [  ] ...



=  + 



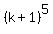
... this reduces to (you can factor 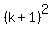 then use a factoring website for the rest) ...  (see NOTE)



= 



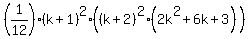
The proof is complete here, but it is not obvious, so

let u=k+1 --> k=u-1



= 

= 



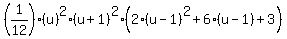
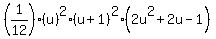
Proof complete



NOTE:  I admit, there may be an easier path here.  If other tutors (or the student) wish to find it, more power to them.  I gave the general idea...



If this helps the student, thanks are appreciated.