Question 1184006: prove using mathematical induction:
1. 1^4 + 2^4 + 3^4 + ... + n^4 = (1/30)n(n+1)(2n+1)(3n^2 + 3n - 1)
Found 2 solutions by math_helper, robertb:
Answer by math_helper(2461)   (Show Source): (Show Source):
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! I will go directly to step 3 of the Inductive process, and will assume the Inductive hypothesis to be true, i.e.,
 for some n = k. for some n = k.
Prove:  is true for n = k + 1, that is, is true for n = k + 1, that is,
 . .
From the inductive hypothesis,

Focus on the the polynomial  , which is of 4th degree. , which is of 4th degree.
By the factor theorem, 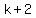 is a factor of this polynomial since is a factor of this polynomial since  . .
Again by the factor theorem, 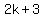 is a factor of this polynomial since is a factor of this polynomial since  . .
In other words,  , where , where  is a quadratic expression. is a quadratic expression.
Now  ===> ===>  ===> ===>  . .
Also, 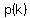 is a 4th degree polynimial whose leading term is is a 4th degree polynimial whose leading term is 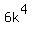 . Since . Since  also, this means also, this means  . .
===> 
===>  ===> ===>  ===> ===>  . .
===>  . .
Therefore,  , ,
and the proof is complete.
|
|
|