Question 1183959: Please help me find the solution set to the inequality
|1 - 4x^2| - |11x - 12 - 2x^2| <= 1.
Thank you.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
By far the easiest way to find the solution set is with a graphing calculator. Graph the two functions
 and and 
and see where the curve is below y=1.

Visually, the solution is the interval between about -6.6 and +1. A graphing calculator gives the approximate interval to several decimal places as (-6.566084, 1.0660844).
An exact algebraic solution requires a lot of work....
The behavior of the function on the left changes when either of the expressions in absolute value changes sign.

The behavior changes are x=-1/2 and x=1/2.
 on the interval (-1/2,1/2); on the interval (-1/2,1/2);
 everywhere else everywhere else

The behavior changes at x=3/2 and x=4.
 on the interval (3/2,4); on the interval (3/2,4);
 everywhere else everywhere else
The critical points of the complete function divide the x-axis into 5 intervals on which the analysis needs to be done separately.
(1) (-infinity,-1/2)
(2) (-1/2,1/2)
(3) (1/2,3/2)
(4) (3/2,4)
(5) (4,infinity)
On intervals (1), (3), and (5),

and the inequality is


The quadratic formula gives the zeros of that quadratic expression as
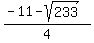 = -6.566084 = -6.566084
and
 = 1.066084 = 1.066084
Note one of those solutions is in interval (1) and the other is in interval (3), so both are valid solutions; and those solutions agree with what we found with a graphing calculator.
I'll let you do the details if you want; but on intervals (2) and (4) there are no real solutions, so the results we have found are the complete answer.
ANSWER: the solution set to the inequality is from 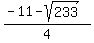 to to 
|
|
|