SOLUTION: Find the domain and range of the function f(x) = (ln(1 - x^2))/√(2x^2 + x - 3).

Algebra ->  Functions -> SOLUTION: Find the domain and range of the function f(x) = (ln(1 - x^2))/√(2x^2 + x - 3).      Log On


   

Question 1183958: Find the domain and range of the function f(x) = (ln(1 - x^2))/√(2x^2 + x - 3).
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
The allowable x values for 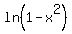ln%281+-+x%5E2%29 are {x ∈ R| 1 > x^2}, or {x ∈ R| 1 > x > -1}, or the open interval (-1,1).
The allowable x values for 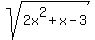sqrt%282x%5E2+%2B+x+-+3%29 are those for which 2x%5E2+%2B+x+-+3+=+%282x+%2B+3%29%28x-1%29+%3E+0, i.e., the interval (-infinity, -3/2) ∪ (1, infinity).

The domain of f(x) would be the intersection of the allowable x values for the top and bottom functions.

That is, (-1,1) ∩ {(-infinity, -3/2) ∪ (1, infinity)} = ∅, the empty set.

Therefore, the domain of the function is the empty set, and consequently the range will be the empty set, too.

NOTE: In practical terms you can actually verify this fact.
The Desmos and Symbolab online graphing utilities will give you an "empty" graph for this function,
that is, all you will see is the x-y coordinate system, and its graph doesn't exist.