Question 1183949: Solve 2x^3 + 3x^2 +hx + k = 0 and find the values of h and k, given that -3 is the first root and the third root is twice the second.
Answer by ikleyn(52795)   (Show Source):
You can put this solution on YOUR website! .
Solve 2x^3 + 3x^2 +hx + k = 0 and find the values of h and k, given that -3 is the first root and the third root is twice the second.
~~~~~~~~~~~~~~~~~
Let x be the second root.
Then the third root is 2x.
Next, according to Vieta's theorem, the ratio of the coefficient at x^2 to the leading coefficient,
i.e. the number  , is the sum of the three roots of the equation, taken with the opposite sign
= -  .
Simplify and find x
3 = -2*((-3) + 3x)
3 = 6 - 6x
6x = 6 - 3
6x = 3
x = 3/6 = 1/2.
Thus, the second root is 1/2; the third root is 1.
According to Vieta's theorem, the ratio 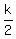 is the product of the three roots taken with the opposite sign
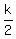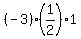= -  = 3/2; hence, k = 3.
According to Vieta's theorem, the ratio 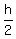 is the sum of in-pairs product of the roots
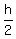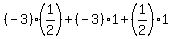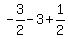=  =  = -4; hence, h = -8
ANSWER. k = 3; h = -8; the second root is  ; the third root is 1.
You can check it on your own, that the found polynomial and its roots satisfy all the conditions imposed by the problem.
Solved.
|
|
|
