|
Question 118383: Find the value of z in the system equations
2x + 3y - 5z = 3
x - 2y + z = 0
3x + y + 3z = 7
using Cramer's rule. answers(0,4/7,1,10/7)
Find the value of x in the system of equations
2x + y - 4 = 0
13x + (5/2)y - 10 = 0
using Cramer's rule. (-2,-1,0,1)
Find the value of y in the system equations
5x - 3y = 18
2x + 4y = 2
using Cramer's rule. (-2,-1,0,1)
Find the value of y in the system of equations
2x + 3y - 5z = 3
x - 2y + z = 0
3x + y + 3z = 7
using Cramer's rule
(0,4/7,1,10/7)
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the value of z in the system equations
2x + 3y - 5z = 3
x - 2y + z = 0
3x + y + 3z = 7
using Cramer's rule. answers(0,4/7,1,10/7)
Write the single letters x, y, and z as
1x, 1y, and 1z, so that like terms in the
three equations all line up vertically:
2x + 3y - 5z = 3
1x - 2y + 1z = 0
3x + 1y + 3z = 7
Form the determinant D by erasing everything
but the coefficients of the letters:
2 + 3 - 5
1 - 2 + 1
3 + 1 + 3
Erase the + signs and move the - signs
closer to the numbers:
2 3 -5
1 -2 1
3 1 3
Then put vertical bars around it:
|2 3 -5|
D = |1 -2 1|
|3 1 3|
Do you know how to find the value of a 3x3 determinant?
I'll assume you do and can find that D = -49.
Now we want to find z, which is the 3rd unknown in the
system, going left to right. Since it is the 3rd unknown,
we form Dz by replacing the 3rd column of D, which is
-5
1
3
by the column of constants, which is
3
0
7
getting
|2 3 3|
Dz = |1 -2 0|
|3 1 7|
and we expand that determinant, getting
Dz = -28
Dz -28
So z = ———— = ————— =  D -49
----------------------------------------------
Find the value of x in the system of equations
2x + y - 4 = 0
13x + (5/2)y - 10 = 0
using Cramer's rule. (-2,-1,0,1)
Write the single letter y as 1y.
2x + 1y - 4 = 0
13x + (5/2)y - 10 = 0
Then get all the letter terms on the left and
all the number terms on the right, so that like
terms in the three equations all line up
vertically:
2x + 1y = 4
13x -
D -49
----------------------------------------------
Find the value of x in the system of equations
2x + y - 4 = 0
13x + (5/2)y - 10 = 0
using Cramer's rule. (-2,-1,0,1)
Write the single letter y as 1y.
2x + 1y - 4 = 0
13x + (5/2)y - 10 = 0
Then get all the letter terms on the left and
all the number terms on the right, so that like
terms in the three equations all line up
vertically:
2x + 1y = 4
13x -  y = 10
Form the determinant D by erasing everything
but the coefficients of the letters:
2 1
13 - y = 10
Form the determinant D by erasing everything
but the coefficients of the letters:
2 1
13 -  Erase the + signs and move the - sign
closer to the number:
2 1
13 -
Erase the + signs and move the - sign
closer to the number:
2 1
13 - Then put vertical bars around it:
| 2 1|
|13 -
Then put vertical bars around it:
| 2 1|
|13 - |
Do you know how to find the value of a 2x2 determinant?
I'll assume you do and can find that D = -18.
Now we want to find x, which is the 1st unknown in the
system, going left to right. Since it is the 1st unknown,
we form Dx by replacing the 1st column of D, which is
2
13
by the column of constants, which is
4
10
getting
Dx = | 4 1|
|10 - |
Do you know how to find the value of a 2x2 determinant?
I'll assume you do and can find that D = -18.
Now we want to find x, which is the 1st unknown in the
system, going left to right. Since it is the 1st unknown,
we form Dx by replacing the 1st column of D, which is
2
13
by the column of constants, which is
4
10
getting
Dx = | 4 1|
|10 - |
and we expand that determinant, getting
Dx = -20
Dx -20
So x = ———— = ————— = |
and we expand that determinant, getting
Dx = -20
Dx -20
So x = ———— = ————— = 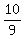 D -18
That's not one of your choices, but it
IS correct anyway. The whole solution
is
x = 10/9, y = 16/9
2x + 1y - 4 = 0
13x +
D -18
That's not one of your choices, but it
IS correct anyway. The whole solution
is
x = 10/9, y = 16/9
2x + 1y - 4 = 0
13x +  y - 10 = 0
2 y - 10 = 0
2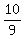 + +  - 4 = 0
13 - 4 = 0
13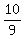 + +   - 10 = 0 - 10 = 0
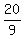 + + 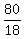 - 4 = 0 - 4 = 0
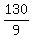 + +  - 4 = 0 - 4 = 0
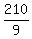 Find the value of y in the system equations
5x - 3y = 18
2x + 4y = 2
using Cramer's rule. (-2,-1,0,1)
Find the value of y in the system of equations
2x + 3y - 5z = 3
x - 2y + z = 0
3x + y + 3z = 7
using Cramer's rule
(0,4/7,1,10/7)
Find the value of y in the system equations
5x - 3y = 18
2x + 4y = 2
using Cramer's rule. (-2,-1,0,1)
Find the value of y in the system of equations
2x + 3y - 5z = 3
x - 2y + z = 0
3x + y + 3z = 7
using Cramer's rule
(0,4/7,1,10/7)
|
|
|
| |