SOLUTION: For arbitrary positive integers k, m, and n, will there exist a prime p such that {{{abs(1/m - n/p) <= k/2^p}}}?

Algebra ->  Divisibility and Prime Numbers -> SOLUTION: For arbitrary positive integers k, m, and n, will there exist a prime p such that {{{abs(1/m - n/p) <= k/2^p}}}?      Log On


   

Question 1183795: For arbitrary positive integers k, m, and n, will there exist a prime p such that abs%281%2Fm+-+n%2Fp%29+%3C=+k%2F2%5Ep?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
No, because m=1, n=1, k=1, is a counter-example.  To show that, we substitute

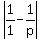
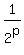abs%281%2F1+-+1%2Fp%29%22%22%3C=%22%221%2F2%5Ep

That only holds when p=1, but 1 is not a prime.

It does not work for the first prime 2

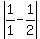
abs%281%2F1+-+1%2F2%29%22%22%3C=%22%221%2F2%5E2
cross%28matrix%281%2C3%2C+1%2F2%2C%22%22%3C=%22%22%2C1%2F4%29%29

And as p increases through larger and larger primes, the left side increases
approaching 1, but the right side decreases approaching 0.  So no larger
integer for p can possibly be a solution, let alone a larger prime number.

Edwin