Question 1183785: Write an equation each of whose roots are 2 less than 3 times the roots of 3x^3 + 10x^2 + 7x - 10 = 0.
Found 3 solutions by MathLover1, ikleyn, robertb:
Answer by MathLover1(20850)   (Show Source):
Answer by ikleyn(52834)  (Show Source):
You can put this solution on YOUR website! .
Write an equation each of whose roots are 2 less than 3 times the roots of 3x^3 + 10x^2 + 7x - 10 = 0
~~~~~~~~~~~~~~~~~~~~~~~
This problem's solution is to apply the Vieta's theorem several times.
Let a, b and c be the roots of the given equation;
let u, v and w be the roots of the projected equation.
According to the condition, we have
u = 3a-2, v = 3b-2, w = 3c-2.
+----------------------------------------------------------------------+
| Let the projected equation be px^3 + qx^2 + rx + s = 0. |
| |
| Our goal is to determine the coefficients p, q, r and s. |
+----------------------------------------------------------------------+
According to Vieta's theorem, a + b + c =  .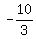
Hence, u + v + w = (3a-2) + (3b-2) + (3c-2) = 3*(a+b+c) - 6 = 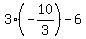 = -10 - 6 = -16.
Thus 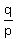 = 16, according to Vieta's theorem.
Next, according to Vieta's theorem, ab + ac + bc =  .
Hence, uv + uw + vw = (3a-2)*(3b-2) + (3a-2)*(3c-2) + (3b-2)*(3c-2) = 9(ab + ac + bc) - (6a + 6b + 6a + 6c + 6b + 6c) + (4+4+4) =
= 9(ab + ac + bc) - 12(a+b+c) + 12 = 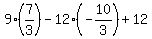 = 21 + 40 + 12 = 73.
Thus 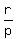 = 73, according to Vieta's theorem.
Finally, according to Vieta's theorem, abc = {{10/3}}}.
Hence, uvw = (3a-2)*(3b-2)*(3c-2) = 27abc - 18(ab + ac + bc) + 12(a + b + c) - 8 =
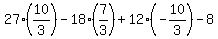=  = 9*10 - 6*7 - 4*10 - 8 = 0.
Thus 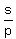 = 0, according to Vieta's theorem.
Since the projected polynomial coefficients ratios are integer numbers, we can take p = 1.
It gives q = 16, r = 73, s = 0.
Thus the projected equation is x^3 + 16x^2 + 73x = 0. ANSWER
Solved.
/\/\/\/\/\/\/\/
The post-solution note
The solution by @MathLover1 works due to that happy occasion, that the given equation has a rational root.
My approach / (my solution) works independently of this occasion.
With my approach, there is no need in finding the roots of the given polynomial.
Answer by robertb(5830)  (Show Source):
You can put this solution on YOUR website! *
The two prior tutors took great details to solve the given problem.
But in fact, the solution is just a simple exercise in transformation of variables.
Suppose that the roots "r" of the equation is transformed into some form g(r).
Let  be the new equation after the roots are transformed.
Then we have  , and  , as long as the inverse function exists and is well-defined.
Since  when the roots are being obtained, we get
 ===>  ===>  , which brings back the roots and the linear factors of the original equation.
Hence, 
becomes the required equation under the new transformation .
In other words, we only have to find the inverse function of  which is  , and substitute into the original equation.
===>  is the new transformed equation.
Then just switch back to the usual "x" variable, giving  .
Note that this result is true whenever the transformation g(x) has a well-defined inverse.
Also, under a general g(x), the resulting equation may not be a polynomial, as what happens when one wants to find the equation
whose roots are cubes of the roots of the original equation. The equation will be  .
-------------------------------------------------------------------------
So no need for hanky panky solutions that don't address the heart of the matter.
Especially from people whose first language is NOT English.
|
|
|
