Question 1183764: Let (x,y) be a point on the triangular region bounded by the line 3x + 4y = 12 and the coordinate axes. Determine the points (x,y) in this region which give the minimum and maximum sums of distances of the point from the line 3x + 4y = 12 and from the coordinate axes. Please include explanation. Thank you!
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let (x,y) be a point on the triangular region bounded by the line 3x + 4y = 12 and the coordinate axes.
Determine the points (x,y) in this region which give the minimum and maximum sums of distances of the point
from the line 3x + 4y = 12 and from the coordinate axes. Please include explanation. Thank you!
~~~~~~~~~~~~~~~~~~~~
Make a sketch.
You have a right triangle ABC with the right angle at vertex A = (0,0);
the point B is x-intercept (4,0) and the point C is y-intercept (0,3).
So the legs of the triangle are AB = 4, BC = 3 and the hypotenuse BC is 5 units long.
Let P = (x,y) be the point inside triangle ABC (including its sides).
Then the distance from P to x-axis is y; the distance from P to y-axis is x.
To find the distance from P to the hypotenuse BC, consider triangles PAB, PAC and PBC.
We will find the distance from P to BC as the altitude of the triangle PBC.
The area of the triangle ABC is  = = 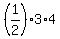 = 6 square units;
the area of the triangle PAB is = 6 square units;
the area of the triangle PAB is 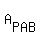 = = 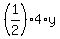 = 2y;
the area of the triangle PBC is = 2y;
the area of the triangle PBC is 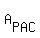 = = 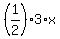 = 1.5x.
The area of the triangle PAC, = 1.5x.
The area of the triangle PAC, 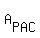 , is the difference , is the difference  - - 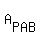 - - 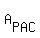 = 6 - 2y - 1.5x.
The altitude of the triangle PBC drawn to BC is TWICE its area divided by the length of BC, i.e. = 6 - 2y - 1.5x.
The altitude of the triangle PBC drawn to BC is TWICE its area divided by the length of BC, i.e. 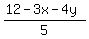 = 2.4 - 0.6x - 0.8y.
Thus, the sum of the distances from the point P(xy) to the sides of the triangle ABC is x + y + 2.4 - 0.6x - 0.8y = 2.4 + 0.4x + 0.2y.
The problem asks to find the points P(x,y) inside the triangle ABC, which provide the minimum / the maximum to this function f(x,y) = 2.4 + 0.4x + 0.2y.
This function is linear function of x and y, and it is not a constant.
THEREFORE, the function gets its maximum/minimum inside the triangle at one of the vertices of the triangle.
So, I prepared the Table below, which shows the value of the function at the vertices of the triangle ABC
T A B L E
f(x,y)
Point A (0,0) 2.4 + 0.4*0 + 0.2*0 = 2.4
Point B (4,0) 2.4 + 0.4*4 + 0.2*0 = 4.0
Point C (0,3) 2.4 + 0.4*0 + 0.2*3 = 3.0
From the Table, the sum of the distances is maximum at the vertex B(4,0).
The sum of the distances is minimum at the vertex A(0,0). = 2.4 - 0.6x - 0.8y.
Thus, the sum of the distances from the point P(xy) to the sides of the triangle ABC is x + y + 2.4 - 0.6x - 0.8y = 2.4 + 0.4x + 0.2y.
The problem asks to find the points P(x,y) inside the triangle ABC, which provide the minimum / the maximum to this function f(x,y) = 2.4 + 0.4x + 0.2y.
This function is linear function of x and y, and it is not a constant.
THEREFORE, the function gets its maximum/minimum inside the triangle at one of the vertices of the triangle.
So, I prepared the Table below, which shows the value of the function at the vertices of the triangle ABC
T A B L E
f(x,y)
Point A (0,0) 2.4 + 0.4*0 + 0.2*0 = 2.4
Point B (4,0) 2.4 + 0.4*4 + 0.2*0 = 4.0
Point C (0,3) 2.4 + 0.4*0 + 0.2*3 = 3.0
From the Table, the sum of the distances is maximum at the vertex B(4,0).
The sum of the distances is minimum at the vertex A(0,0).
Solved, answered and thoroughly explained.
/////////////
I just fixed my error after notice by @greenestamps, and now you see the fixed correct version.
Thanks to @greenestamps !
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor contains errors, which I am sure she will find and correct after seeing that I have provided a response to your question.
The given triangle has vertices (0,0), (4,0), and (0,3).
Let the point P (x,y) be in that triangle.
The distance of P from the x-axis is y; the distance from the y-axis is x.
The distance of P from the line 3x+4y=12, or 3x+4y-12=0, is

For all points inside the triangle,
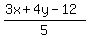
is negative. So
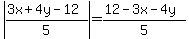
and the sum of the distances of P from the three sides of the triangle is

Given that expression for the sum of the distances of P from the three sides of the triangle, it is clear that the minimum sum is at (0,0), where the sum of the distances is 12/5.
For the maximum sum, note that for a given value of x the sum of the distances is greatest is when y is as large as possible; and for a given value of y the sum of the distances is greatest is when x is as large as possible. That means the maximum sum is when the point P is somewhere on the boundary line 3x+4y=12.



The sum of the distance is then

And clearly the maximum value of that expression is when x is as large as possible -- at (4,0).
The maximum sum is then
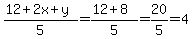
ANSWERS:
minimum sum 12/5 = 2.4, at (0,0)
maximum sum 4, at (4,0)
|
|
|