Question 1183756: The quality assurance engineer of a receiving-sets manufacturer inspects receiving-sets in lots of 50. He selects 5 of the 50 receiving-sets at random and inspects them thoroughly. Assuming that 6 of the 50 receiving-sets in the current lot are defective, find the probability that exactly 2 of the 5 receiving-sets selected by the engineer are defective.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the probability of a set being defective is 6/50 = .12.
the probability of a wet not being defective is 1 - .12 = .88
you select 5 of the 50 at random.
the formula to use is p(x) = p^x * q^(n-x) * c(n,x).
p is the probability of the set being defective.
q is the probability of the set not being defective.
n is equal to 5.
x is equal to 0 to 5.
c(n,x) is equal to n! / (x! * (n-x)!).
you want the probability that exactly 2 of the 5 sets selected at random are defective.
p(2) = .12^2 * .88^(5-2) * c(5,2) = .12^2 * .88^3 * c(5,2) = .12^2 * .88^3 * 10 = .098131968.
that should be your answer.
all the probabilities are shown below:

the eum of all probabilities is equal to 1, as it should be.
probability of exactly 2 defective sets is p(2) = .098131968, which is equal to .098132 when rounded to 6 decimal digits.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The quality assurance engineer of a receiving-sets manufacturer inspects receiving-sets in lots of 50.
He selects 5 of the 50 receiving-sets at random and inspects them thoroughly.
Assuming that 6 of the 50 receiving-sets in the current lot are defective,
find the probability that exactly 2 of the 5 receiving-sets selected by the engineer are defective.
~~~~~~~~~~~~~~~~~~~
I solved a TWIN problem several days ago under this link
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1183648.html
Now, I copy-paste that solution and change/recalculate the numbers in it accordingly.
P = 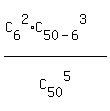 = = 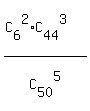 = = 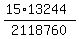 = 0.0093762. ANSWER
The numerator of P, = 0.0093762. ANSWER
The numerator of P, 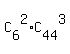 , is the number of favorable combinations of 5 of the 50 receiving-sets,
that contain exactly 2 defective receiving-sets and 3 good receiving-set.
It is the favorable set.
The denominator is the total number of 5 receiving-sets selected by the engineer from 50 receiving-sets.
The probability, as always in such problem, is the ratio , is the number of favorable combinations of 5 of the 50 receiving-sets,
that contain exactly 2 defective receiving-sets and 3 good receiving-set.
It is the favorable set.
The denominator is the total number of 5 receiving-sets selected by the engineer from 50 receiving-sets.
The probability, as always in such problem, is the ratio  . .
Solved.
-----------------
To see many other similar (and different) solved problems, look into the lessons
- Elementary Probability problems related to combinations
- Elementary Probability problems related to combinations REVISITED
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Solved problems on Probability".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Consider these lessons as your textbook, handbook, a Solutions Manual, tutorials and (free of charge) home teacher.
Happy learning (!)
/////////////
The solution by @Theo is incorrect.
He mistakenly assumed that the problem is on Binomial distribution.
In reality, it is not so.
|
|
|