 The polynomial
The polynomial  takes on the value
takes on the value
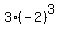
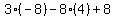
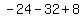
 when x=-2
The polynomial
when x=-2
The polynomial  also has derivative
also has derivative
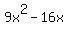 and when x=-2, the derivative is
and when x=-2, the derivative is
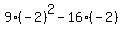
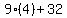
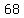 So the line
So the line  must join the polynomial
must join the polynomial  at the point (-2,-48) in order for f(x) to be continuous there.
Also the line must have the same slope as the polynomial has
derivative there.
y = ax + b has slope a, so we have a=68
y = 68x + b
and it must pass through (-2,-48), so we substitute:
-48 = 68(-2) + b
-48 = -136 + b
88 = b
So a = 68 and b = 88.
Edwin
at the point (-2,-48) in order for f(x) to be continuous there.
Also the line must have the same slope as the polynomial has
derivative there.
y = ax + b has slope a, so we have a=68
y = 68x + b
and it must pass through (-2,-48), so we substitute:
-48 = 68(-2) + b
-48 = -136 + b
88 = b
So a = 68 and b = 88.
Edwin