Question 1183685: Consider the quarter-ellipse x^2/9 + y^2/4 = 1 at the 1st quadrant. Two points (0,1/2) and (2,0) are fixed on the y- and x-axes, respectively.
A third point (x,y) is allowed to move along the quarter-ellipse, forming a triangle with the two other given points. Determine the coordinates of the point (x,y) on the curve which will give the triangle with
(i) The optimal area;
(ii) The optimal perimeter.
Found 3 solutions by Alan3354, robertb, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider the quarter-ellipse x^2/9 + y^2/4 = 1 at the 1st quadrant. Two points (0,1/2) and (2,0) are fixed on the y- and x-axes, respectively.
A third point (x,y) is allowed to move along the quarter-ellipse, forming a triangle with the two other given points. Determine the coordinates of the point (x,y) on the curve which will give the triangle with
(i) The optimal area;
(ii) The optimal perimeter.
======================================
optimal
---
noun, plural op·ti·ma [op-tuh-muh], op·ti·mums.
the best or most favorable point, degree, amount, etc., as of temperature, light, and moisture for the growth or reproduction of an organism.
the greatest degree or best result obtained or obtainable under specific conditions.
---------------------------
Did you mean maximum?
or minimum?
Optimal is meaningless.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! *
 : To tutor ikleyn's comment: "To include proof would be BAD STYLE for this brilliant idea. : To tutor ikleyn's comment: "To include proof would be BAD STYLE for this brilliant idea.
Also, I can not refer to any source, because I didn't see this idea NOWHERE and NEVER before." IDEAS CAN BE WRONG!!!
That's why there are proofs in mathematics.
If she says this then she is NOT A GOOD TEACHER, and she is setting a very bad example. She has no choice but to give it a formal proof.
As it stands she has to connect the idea of the derivative at a point on the curve with the optimal consequence of the problem.
No proof, no truth. Understand my comments.
So, for the sake of the students, I say again: At best, ikleyn's solution IS  and and  . .
------------------------------------------------------------------------
 : The tutor ikleyn claims that the 3rd vertex of the triangle giving the max area "... is located on the straight line, : The tutor ikleyn claims that the 3rd vertex of the triangle giving the max area "... is located on the straight line,
PARALLEL [caps mine] to segment AB and TANGENT [caps mine] to the ellipse." Although this seems true at first sight,
it is a statement that needs proof or citation.
The reason for this being, solely judging the magnitude of the area by the lenth of the altitude, the statement would have to consider
(i) unaccounted parts of the quarter ellipse (particularly its left and right ends where an altitude doesn't intersect), requiring her to consider
(ii) triangles which are OUTSIDE the quarter-ellipse itself, contrary to the condition of the problem.
So at best, her solution remains CIRCUMSTANTIAL and INCOMPLETE.
*
I will solve only part (i) with enough amount of info so you will know how to attack the problem in part (ii), which has a similar approach.
(i) Since the point (x,y) is on the quarter-ellipse  at the first quadrant, we have (x,y) = (x, at the first quadrant, we have (x,y) = (x, 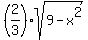 ). ).
Thus, the triangle has vertices (0, 1/2), (2,0), and (x, 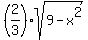 ), where the third is free to vary in the interval [0, 3]. ), where the third is free to vary in the interval [0, 3].
The area of the triangle, interms of the coordinates of its vertices is given by

===>  . .
Set  to get the critical values. to get the critical values.
 ===> ===>  . .
===>  <===> <===>  ==> ==>  . .
===>  ~ 1.05337 (5 d.p.). Choose the positive solution since this is the value that's between 0 and 3. ~ 1.05337 (5 d.p.). Choose the positive solution since this is the value that's between 0 and 3.
If  , then , then 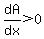 (i.e., A is increasing) (i.e., A is increasing)
If 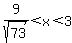 , then , then 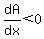 (i.e., A is decreasing) (i.e., A is decreasing)
Then by the first derivative test, there is a local max at  . .
To find the absolute max and abs min areas, compare the area value at  with those of the area values at the end points. with those of the area values at the end points.

 <---- minimum area <---- minimum area
 to 3 d.p. <---- max area to 3 d.p. <---- max area
---------------------------------------------------------------------
This is as far as I go. If you need help in part (ii), message me, but I will only help you in setting up the equation for the perimeter of the triangle.
It is good training for you to be able to do a problem like this (which is the whole point of the homework).
Answer by ikleyn(52752)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Consider the quarter-ellipse x^2/9 + y^2/4 = 1 at the 1st quadrant. Two points (0,1/2) and (2,0) are fixed
on the y- and x-axes, respectively.
A third point (x,y) is allowed to move along the quarter-ellipse, forming a triangle with the two other given points.
Determine the coordinates of the point (x,y) on the curve which will give the triangle with
(i) The maximum area;
(ii) The maximum perimeter.
~~~~~~~~~~~~~~~
There is nice geometric idea and simple way to solve the problem ( part (i) ).
Inside the ellipse, we are given the segment AB with endpoints A = (0,1/2) and B = (2,0).
This segment is one of the side of the sough triangle with the maximum area.
Geometrically, it is clear that the area of such triangle is maximum when its altitude, drawn to side AB, has maximum possible length.
In turn, it makes it clear that the opposite vertex of such triangle is located on the straight line, parallel to segment AB and tangent to the ellipse.
It reduces the problem to finding the tangent line to the ellipse, parallel to the segment AB.
+------------------------------------------------------------------+
| Thus the way is open, and we only need implement this idea. |
+------------------------------------------------------------------+
The slope of segment AB is m =  = =  .
From the ellipse equation .
From the ellipse equation 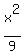 + +  = =  , we have the formula for "y" y = , we have the formula for "y" y = 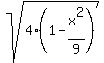 .
Therefore, the derivative y' is
y' = .
Therefore, the derivative y' is
y' =  = = 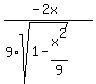 .
We want the derivative to be equal to the slope of AB, which is .
We want the derivative to be equal to the slope of AB, which is  . It gives this equation . It gives this equation
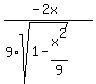 = =  .
Cross-multiply
8x = .
Cross-multiply
8x = 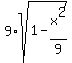 ;
square both sides
64x^2 = ;
square both sides
64x^2 =  and simplify
64x^2 = 81 - 9x^2
64x^2 + 9x^2 = 81
73x^2 = 81 ---> x^2 = 81/73 ---> x =
and simplify
64x^2 = 81 - 9x^2
64x^2 + 9x^2 = 81
73x^2 = 81 ---> x^2 = 81/73 ---> x = 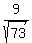 .
Now the corresponding coordinate "y" is
y = .
Now the corresponding coordinate "y" is
y = 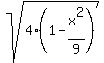 = = 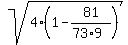 = = 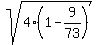  = =  .
Thus the third vertex of the triangle is C = (x,y) = ( .
Thus the third vertex of the triangle is C = (x,y) = (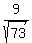 , , ). ANSWER ). ANSWER
-------------
Regarding the note by @robertb requiring proof or citation my statement,
it is actually SELF-EVIDENT statement (after it came to the mind), and THEREFORE does not need proof or citation.
To include proof would be BAD STYLE for this brilliant idea.
Also, I can not refer to any source, because I didn't see this idea NOWHERE and NEVER before.
And finally, I wrote my solution for the reader, who is adequate to the problem.
|
|
|