Question 1183648: The quality assurance engineer of a receiving-sets manufacturer inspects receiving-sets in lots of 50. He selects 4 of the 50 receiving-sets at random and inspects them thoroughly. Assuming that 5 of the 50 receiving-sets in the current lot are defective, find the probability that exactly 3 of the 4 receiving-sets selected by the engineer are defective.
Answer by ikleyn(52884)   (Show Source):
You can put this solution on YOUR website! .
The quality assurance engineer of a receiving-sets manufacturer inspects receiving-sets in lots of 50.
He selects 4 of the 50 receiving-sets at random and inspects them thoroughly.
Assuming that 5 of the 50 receiving-sets in the current lot are defective, find the probability
that exactly 3 of the 4 receiving-sets selected by the engineer are defective.
~~~~~~~~~~~~~~~~~~~~~~
P =  =  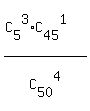=  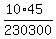=  = 0.001954. ANSWER
The numerator of P,  , is the number of favorable combinations of 4 of the 50 receiving-sets,
that contain exactly 3 defective receiving-sets and one good receiving-set.
It is the favorable set.
The denominator is the total number of 4 receiving-sets selected by the engineer from 50 receiving-sets.
The probability, as always in such problem, is the ratio  .
Solved.
-----------------
To see many other similar (and different) solved problems, look into the lessons
- Elementary Probability problems related to combinations
- Elementary Probability problems related to combinations REVISITED
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Solved problems on Probability".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
Consider these lessons as your textbook, handbook, a Solutions Manual, tutorials and (free of charge) home teacher.
Happy learning (!)
|
|
|
