|
Question 1183640: A man leaves his house at 8:00 AM and traveling at an average speed of 2 kph, arrives at his office 3 min ahead of the expected time. Had he left his house at 8:30 am and traveled at an average speed of 3 kph, he will arrive 6 min late of the expected time. Find the distance that he had traveled.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A man leaves his house at 8:00 AM and traveling at an average speed of 2 kph, arrives at his office
3 min ahead of the expected time. Had he left his house at 8:30 am and traveled at an average speed of 3 kph,
he will arrive 6 min late of the expected time. Find the distance that he had traveled.
~~~~~~~~~~~~~~~~~~
As the problem is worded, it may perplex the reader.
To avoid perplexing, I'd re-formulate the condition this way:
A man leaves his house at 8:00 AM and traveling at an average speed of 2 kph, arrives at his office
3 min ahead of the  scheduled time.
Had he left his house at 8:30 am and traveled at an average speed of 3 kph,
he will arrive 6 min late of the scheduled time.
Had he left his house at 8:30 am and traveled at an average speed of 3 kph,
he will arrive 6 min late of the  scheduled time.
Find the distance that he had traveled. scheduled time.
Find the distance that he had traveled.
SOLUTION
Let d be the distance from the house to the office.
The travel time in the first scenario is  hours.
The travel time in the second scenario is hours.
The travel time in the second scenario is 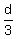 hours.
The difference of the travel times is (t - 8:00 - 3) - ((t+6) - 8:30) = 30 -3 - 6 = 21 minutes, or hours.
The difference of the travel times is (t - 8:00 - 3) - ((t+6) - 8:30) = 30 -3 - 6 = 21 minutes, or  of an hour,
where "t" is the scheduled time clock reading.
It gives the time equation of an hour,
where "t" is the scheduled time clock reading.
It gives the time equation
 - - 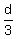 = =  hours
to find "t". To solve the equation, multiply both sides by 60. You will get
30d - 20d = 21
10d = 21
d = 21/10 = 2.1 miles. ANSWER
ANSWER. The distance from home to the office is 2.1 miles.
CHECK. The travel time in the first scenario is hours
to find "t". To solve the equation, multiply both sides by 60. You will get
30d - 20d = 21
10d = 21
d = 21/10 = 2.1 miles. ANSWER
ANSWER. The distance from home to the office is 2.1 miles.
CHECK. The travel time in the first scenario is  = 1.05 hours = 1 hour and 3 minute.
Hence, the appointment time (scheduled arriving time) is 9:06 am.
In the second scenario, his travel time was = 1.05 hours = 1 hour and 3 minute.
Hence, the appointment time (scheduled arriving time) is 9:06 am.
In the second scenario, his travel time was  = 0.7 of an hour, or 42 minutes;
he started at 8:30 am, hence, he arrived at 9:12 am, which is 6 minutes later
than the scheduled arriving time of 9:06 am.
! Correct ! = 0.7 of an hour, or 42 minutes;
he started at 8:30 am, hence, he arrived at 9:12 am, which is 6 minutes later
than the scheduled arriving time of 9:06 am.
! Correct !
Solved.
|
|
|
| |