SOLUTION: Solve the inequality |x - 2| <= |3x + 12| + 2.

Algebra ->  Inequalities -> SOLUTION: Solve the inequality |x - 2| <= |3x + 12| + 2.       Log On


   

Question 1183626: Solve the inequality
|x - 2| <= |3x + 12| + 2.
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Let's solve your inequality step-by-step.
abs%28x-2%29%3C=+abs%283x%2B12%29%2B2

Let's find the critical points of the inequality.

|abs%28x-2%29%3C=+abs%283x%2B12%29%2B2

Either x-2=abs%283x%2B12%29%2B2 or x-2=-%28abs%283x%2B12%29%2B2%29

Part 1:
x-2=abs%283x%2B12%29%2B2............(Flip the equation)
abs%283x%2B12%29%2B2=x-2...........(Add -2 to both sides)
abs%283x%2B12%29%2B2-2=x-2-2
abs%283x%2B12%29=x-4

We know either 3x%2B12=x-4 or 3x%2B12=-%28x-4%29

3x%2B12=x-4...............(Possibility 1)
3x%2B12-x=x-4-x........... (Subtract x from both sides)
2x%2B12=-4
2x%2B12-12=-4-12............ (Subtract 12 from both sides)
2x=-16
2x%2F2=-16%2F2............ (Divide both sides by 2)
x=-8

3x%2B12=-%28x-4%29........... (Possibility 2)
3x%2B12=-x%2B4............ (Simplify both sides of the equation)
3x%2B12%2Bx=-x%2B4%2Bx................ (Add x to both sides)
4x%2B12=4
4x%2B12-12=4-12.................... (Subtract 12 from both sides)
4x=-8
4x%2F4=-8%2F4........ (Divide both sides by 4)
x=-2

Check answers. (Plug them in to make sure they work.)
x=-8+=>Doesn't work in original equation
x=-2+=>Doesn't work in original equation

Part 2:
+x-2=-%28abs%283x%2B12%29%2B2%29 ............(Flip the equation)
-%28abs%283x%2B12%29%2B2%29=x-2
-abs%283x%2B12%29-2%2B2=x-2%2B2......... (Add 2 to both sides)
-abs%283x%2B12%29=x
-abs%283x%2B12%29%2F-1=x%2F-1 .............(Divide both sides by+-1)
abs%283x%2B12%29=-x

We know either 3x%2B12=-x or 3x%2B12=-%28-x%29

3x%2B12=-x+..................+++%28Possibility+1%29%0D%0A%0D%0A%7B%7B%7B3x%2B12%2Bx=-x%2Bx.......... (Add x to both sides)
4x%2B12=0
4x%2B12-12=0-12........... (Subtract 12 from both sides)
4x=-12
4x%2F4=-12%2F4......... (Divide both sides by 4)
x=-3

3x%2B12=-%28-x%29............. (Possibility 2)
3x%2B12=x............ (Simplify both sides of the equation)
3x%2B12-x=x-x.................... (Subtract+x from both sides)
2x%2B12=0
2x%2B12-12=0-12.............(Subtract 12 from both sides)
2x=-12
2x%2F2=-12%2F2........... (Divide both sides by+2)
x=-6

Check answers. (Plug them in to make sure they work.)
x=-3=> Works in original equation.
x=-6 =>Works in original equation.

Critical points:
x=-3 or+x=-6
Check intervals in between critical points. (Test values in the intervals to see if they work.)
x%3C=-6+=>Works in original inequality.
-6%3C=x%3C=-3+=> Doesn't work in original inequality.
x%3E=-3 =>Works in original inequality.
Answer:
x%3C=-6+ or x%3E=-3

Answer by greenestamps(13215) About Me  (Show Source):
You can put this solution on YOUR website!


abs%28x-2%29%3C=abs%283x%2B12%29%2B2

Probably the easiest way to find the solution set is to graph the two expressions with a graphing calculator.

red: abs%28x-2%29
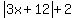
green: abs%283x%2B12%29%2B2

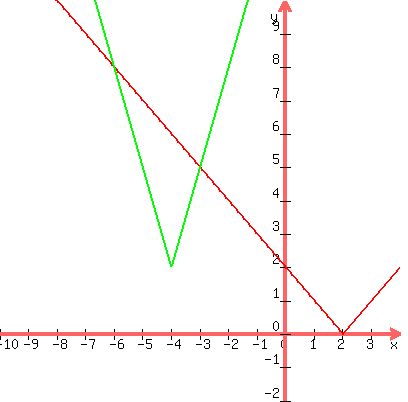
graph%28400%2C400%2C-10%2C4%2C-2%2C10%2Cabs%28x-2%29%2Cabs%283x%2B12%29%2B2%29

We can see from the graph that the solution set (red line below green line) is (-infinity, -6] U [-3,infinity).

For an algebraic solution, I prefer a different method than the one shown by the other tutor....

The behaviors of the two functions change when (x-2) is zero and when (3x+12) is zero -- at x = -4 and x=2. So separate the analysis into three intervals:
(1) (-infinity,-4]
(2) [-4,2]
(3) [2,infinity)

(1) On (-infinity,-4]...
abs%28x-2%29=-x%2B2
abs%283x%2B12%29%2B2=-3x-12%2B2=-3x-10

-x%2B2%29%3C=-3x-10
2x%3C=-12
x%3C=-6

All the x values in that range are in the interval for this case, so part of the solution set is (-infinity,-6].

(2) On [-4,2]...
abs%28x-2%29=-x%2B2
abs%283x%2B12%29%2B2=3x%2B12%2B2=3x%2B14

-x%2B2%3C=3x%2B14
-12%3C=4x
x%3E=-3

For x values in the interval for this case, [-4,2], only the values x>=-3 satisfy the inequality. So another part of the solution set is [-3,2].

(3) On [2,infinity)...
abs%28x-2%29=x-2
abs%283x%2B12%29%2B2=3x%2B12%2B2=3x%2B14

x-2%3C=3x%2B14
-16%3C=2x
x%3E=-8

All the x values in that range are in the interval for this case, so part of the solution set is [2,infinity).

Combining the solutions sets for the three cases we get the answer we saw from the graph: (-infinity,-6] U [-3,infinity)