Question 1183622: In the diagram shown in the image, what is the area, in square units, of right triangle ABC with right angle ∠ABC. A link to the image: https://imgur.com/a/EhwZzKH
Found 3 solutions by MathLover1, ikleyn, greenestamps:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem, and many other similar problems, can be solved in one line without calculating the side lengths
of the triangles, without using the distance formula and without calculating square roots.
Moreover, it can be solved MENTALLY.
Take the minimal rectangle in the coordinate plane with the sides parallel to x- and y-axes,
which covers (contains) the given triangle.
The sides of such a rectangle are 4 units horizontally and 4 units vertically, which is clear from the plot.
Next, from the area of this rectangle, which is 4*4 = 16 square units, subtract the areas of the three excessive triangles.
The areas of excessive triangles are  = 1 square unit; = 1 square unit; 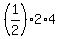 = 4 square units; and = 4 square units; and 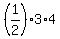 = 6 square units.
So, the area of the triangle ABC is 16 - 1 - 4 - 6 = 5 square units. ANSWER = 6 square units.
So, the area of the triangle ABC is 16 - 1 - 4 - 6 = 5 square units. ANSWER
Solved.
------------
It is a classic entertainment problem to solve it mentally.
Notice that my solution does not use the fact that the given triangle is a right-angled triangle.
The solution works for any triangle with the vertices at the nodes of an integer grid on a coordinate plane.
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The first tutor used the easily observable fact that angle B is a right angle to find the area as one-half the product of the lengths of the two legs.
The second tutor used a standard method of enclosing the triangle in a rectangle and finding the area of the triangle as the area of the rectangle minus the area inside the rectangle but outside of the triangle.
Here are a couple of other ways to solve the problem.
(1) Let D be the y-intercept of side AC;
determine that the length of BD is 2.5;
then find the area of ABC as the sum of the areas of triangle CBD and ABD -- both of which are triangles with base 2.5 and height 2:
A = 2(1/2)(5/2)(2) = 5
(2) And here is a method that is very powerful in that it can be used to find the area of ANY polygon using the coordinates of the vertices. This is popularly known as the shoelace method.
Step 1: Write the coordinates of the vertices in two columns, making sure to go around the polygon in the correct order; and repeating the first vertex as the last entry in the column. (Note with a triangle it is not possible to list the coordinates in the wrong order....)
0 1
-2 0
2 -3
0 1
Step 2: Moving down to the right, multiply pairs of coefficients; then, moving down right to left, multiply pairs of coefficients. The diagram shows why the process gets the name shoelace method.
0 1
\/
/\
-2 0
/ \/ \
-2 /\ 0
2 -3
/ \/ \
0 /\ 6
0 1
/ \
0 2
Step 3: The area is half the absolute value of the difference between the sums in the two columns of products:

|
|
|