SOLUTION: Need help with solving this system of Trig equations: r = a sin(x) r = a cos(2x)

Left sides of the two equations are identical - hence, their right sides are equal

    a*sin(x) = a*cos(2x)


Cancel the common factor "a" in both sides (assuming a =/= 0).  Then

    sin(x) = cos(2x)      (1)



    +-------------------------------------------------------+
    |    From this point, there are two ways to proceed.    |
    +-------------------------------------------------------+



One way is to notice that equation (1) implies  

    x + 2x = 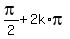  for any integer  k = 0, +/-1, +/-2, . . . 


It gives further

      3x  = ,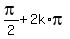

       x  = ,


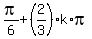which gives 3 (three) geometrically different answers for x

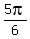       x  =  = 30°  (at k=0);   x =  = 150°  (at k=1)   and   x =   = 270°  (at k=2).   (2)


At this point, first way solution is complete.



Another way to solve equation (1) is to replace the right side cos(2x) by 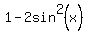, using well known trigonometric identity.


You will get then the equation

    sin(x) = ,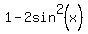

or

     = 0.


It is a quadratic equation for sin(x). You can solve it  EITHER  using the quadratic formula  OR  factoring

     = (2sin(x)-1)*(sin(x)+1).


Doing this way, you will obtain the solutions

    sin(x) =   or  sin(x) = -1,

which lead to the same answers as the found above in (2).