SOLUTION: The expression ax^3 + bx^2 - 5x + 2a is exactly divisible by x^2 - 3x - 4. Calculate the value of a and of b and factorise the expression completely.

Algebra ->  Test -> SOLUTION: The expression ax^3 + bx^2 - 5x + 2a is exactly divisible by x^2 - 3x - 4. Calculate the value of a and of b and factorise the expression completely.      Log On


   

Question 1183613: The expression ax^3 + bx^2 - 5x + 2a is exactly divisible by x^2 - 3x - 4. Calculate the value of a and of b and factorise the expression completely.
Found 3 solutions by KMST, ikleyn, greenestamps:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2-3x-4=%28x%2B1%29%28x-4%29 tells us
1) two of the factors we need to "factorise the expression completely" and
2) that the expression is zero for x=-1 and for x=4 .
ONE OPTION:
Using the second finding we know that
a%28-1%29%5E3%2Bb%28-1%29%5E2-5%28-1%29%2B2a=0 --> -a%2Bb%2B5%2B2a=0 --> a%2Bb%2B5=0 and
a%284%29%5E3%2Bb%284%29%5E2-5%284%29%2B2a=0 --> 64a%2B16b-20%2B2a=0 --> 66a%2B16b-20=0
We can then solve the system of equations
system%28a%2Bb%2B5=0%2C66a%2B16b-20=0%29 or system%28a%2Bb=-5%2C66a%2B16b=20%29
to find
system%28a=2%2Cb=-7%29 ;
then re-write the original expression/polynomial as
2x%5E3-7x%5E2-5x%2B4 ,
and then find the other factor(s) we need to "factorise the expression completely" as
%282x%2Bc%29%28x%2B1%29%28x-4%29 or as 2%28x-r%29%28x%2B1%29%28x-4%29 ,
depending on what is understood by factorise completely.
The missing factor(s) can be found by
1) dividing the original expression by x%5E2-3x-4 , or by
2) dividing in two steps by %28x%2B1%29 and then by %28x-4%29 , or by
3) multiplying %282x%2Bc%29%28x%5E2-3x-4%29 or as 2%28x-r%29%28x%5E2-3x-4%29
and knowing that identical expressions means equal for every value of the variable, comparing to
2x%5E3-7x%5E2-5x%2B4
to conclude that the the two ways to express the independent term mean
-4c=4 --> c=-1 or 2r=4 --> r=1%2F2

ANOTHER OPTION:
Multiply %28ax%2Bc%29%28x%5E2-3x-4%29 or as a%28x-r%29%28x%5E2-3x-4%29
and match the expressions of the coefficients in that product to the coefficients in
ax%5E3+%2B+bx%5E2+-+5x+%2B+2a to find a , b , and either c or r
For example:
%28ax%2Bc%29%28x%5E2-3x-4%29%22=%22ax%5E3-3ax%5E2-4ax%2Bcx%5E2-3cx-4c
%22=%22ax%5E3%2B%28-3a%2Bc%29x%5E2%2B%28-4a-3c%29x-4c gives you
system%28a=a%2Cb=-3a%2Bc%2C-5=-4a-3c%2C2a=-4c%29 or system%28-5=-4a-3c%2C2a=-4c%29 and b=-3a%2Bc
which tells you
system%28a=2%2Cc=-1%29 and substituting into b=-3a%2Bc you get b=-7

Answer by ikleyn(52921) About Me  (Show Source):
You can put this solution on YOUR website!
.
The expression ax^3 + bx^2 - 5x + 2a is exactly divisible by x^2 - 3x - 4.
Calculate the value of a and of b and factorise the expression completely.
~~~~~~~~~~~~~


            Tutor @KMST provided very detailed long solution,  covering different possible options.
            I will try to give shorter solution in hope that it has its own charm. 


The trinomial  x^2 - 3x - 4  is factorable:  x^2 - 3x - 4 = (x-4)*(x+1).


It means that the given polynomial of the degree 3,  ax^3 + bx^2 - 5x + 2a,  is divisible 
by both binomials  (x-4)  and  (x+1).


Due to the Remainder theorem, it means that the values x= 4  and  x= -1  are the roots of that polynomial.


So, we substitute the values x= 4  and  x= -1 into the given polynomial, equate it to zero and
obtain two equations for the unknown coefficients  "a"  and  "b"


    a*4^3    + b*4^2 - 5*4    + 2a = 0      (1)

    a*(-1)^3 + b*1^2 - 5*(-1) + 2a = 0      (2)


Simplifying, you get


    64a + 16b - 20 + 2a = 0                 (1')

    -a  +   b +  5 + 2a = 0                 (2')


Simplifying further, you get

    66a + 16b = 20                          (1'')

      a +   b = -5                          (2'')
   

After solving the system, you get  a= 2,  b= -7.


Now the problem requires to find the third linear binomial, which is a third divisor to the given polynomial.


Use the Vieta's theorem:  the sum of the roots is equal to  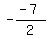-b%2Fa = -%28-7%29%2F2 = 7%2F2.

    so, we write  4 + (-1) + t = 7%2F2


where "t" is the third root, and we obtain from it

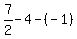    t = 7%2F2+-+4+-+%28-1%29 = 1%2F2.


Thus the third root is  1%2F2, the associate binomial factor is  (x-1/2), and the required binomial decomposition is

    ax^3 + bx^2 - 5x + 2a = 2x^3 -7x^2 - 5x + 4 = 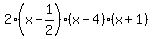2%2A%28x-1%2F2%29%2A%28x-4%29%2A%28x%2B1%29 = (2x-1)*(x-4)*(x+1).

Solved.



Answer by greenestamps(13216) About Me  (Show Source):
You can put this solution on YOUR website!


And here is a third and very different way to solve the problem....

We need to have

%28px%2Bq%29%28x%5E2-3x-4%29=ax%5E3%2Bbx%5E2-5x%2B2a

Perform the multiplication on the left...

px%5E3%2B%28q-3p%29x%5E2%2B%28-4p-3q%29x%2B%28-4q%29

... and equate coefficients:

x^3: p=a [1]
x^2: q-3p=b [2]
x: -4p-3q=-5 [3]
constant: -4q=2a --> q=-0.5a [4]

We have 4 equations in 4 unknowns, which could have led to a messy solution. But things work out nicely....

Substitute [1] and [4] into [3]:
-4a+1.5a=-5
-2.5a=-5
a=2

Then
p=a=2
q=-0.5a = -1
b = q-3p=-1-6=-7

ANSWER: a=2; b=-7 (and p=2; q=-1)

CHECK:
%282x-1%29%28x%5E2-3x-4%29=2x%5E3-7x%5E2-5x%2B4=ax%5E3%2Bbx%5E2-5x%5E2%2B2a%29