Question 1183595: The sum of the two whole numbers is 45 and their difference is less than 10. The number of all possible pairs is???
Found 3 solutions by ankor@dixie-net.com, greenestamps, Solver92311:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The sum of the two whole numbers is 45
x + y = 45
y = (45-x)
and their difference is less than 10.
x - y < 10
x < y + 10
x < (45-x) + 10
2x < 55
x < 55/2
x < 27.5
x = 27
The number of all possible pairs is???
x=27, y=18, a diff of 9
x=26, y=19, a diff of 7
x=25, y=20, a diff of 5
x=24, y=21, a diff of 3
x=23, y=22, a diff of 1
5 pairs possible with, using only positive number differences
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Logically, if the sum of two whole numbers is 45, then one of them is even and the other is odd.
If two whole numbers are one even and the other odd, then their difference is an odd number.
Since the problem requires that the difference between the two numbers be less than 10, the difference can be either 1, 3, 5, 7, or 9.
So there are 5 pairs of whole numbers that satisfy the conditions of the problem.
ANSWER: 5
Algebraically....
Let the larger number be x and the smaller be y.


Solve the first equation for y:

Substitute in the inequality:

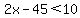
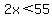
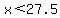
The larger number has to be less than 27.5, so the largest it can be is 27.
That's as far as the algebraic solution gets you; you still have to do some logical reasoning to find the answer to the problem.
Since x is the larger of the two numbers, it has to be greater than 45/2=22.5, so the smallest it can be is 23.
That means the larger number can be any whole number between 23 and 27, inclusive; that is 5 numbers.
Answer by Solver92311(821)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The thing is, given the more restrictive definition of Whole Numbers, i.e., the non-negative integers, neither of the numbers can be negative, but there is absolutely nothing about the problem that either says or implies that the difference must be non-negative. Hence, using the more restrictive definition, the first number could well be zero and the second 45, making a difference of -45 which is most certainly less than 10. Therefore the range of the first number is 0 to 27 and the range of the second is 18 to 45.
John

My calculator said it, I believe it, that settles it

From
I > Ø

|
|
|