Question 1183585: Owen is jumping on a trampoline. When his feet hit the deck of the trampoline, the material depresses to a minimum height of 2cm. On average, Owen is reaching a maximum height of 200cm every 10 seconds. Determine the equation of a sinusoidal function that would model this situation, assuming Owen reaches his first maximum at 6 seconds.
Answer by ikleyn(52858)   (Show Source):
You can put this solution on YOUR website! .
Owen is jumping on a trampoline. When his feet hit the deck of the trampoline,
the material depresses to a minimum height of 2cm.
On average, Owen is reaching a maximum height of 200cm every 10 seconds.
Determine the equation of a sinusoidal function that would model this situation, assuming Owen reaches his first maximum at 6 seconds.
~~~~~~~~~~~~~~
I will not consider the physical processes described in the post.
I will re-formulate Math problem formally.
Restore a sinusoidal function based on following data:
- the minimum height is 2 cm; the maximum height is 200 cm;
- the period is 10 seconds;
- the body is in its upper position at t= 6 seconds.
SOLUTION
The midline is half-way between y= 2 cm and y= 200 cm, so midline is y = 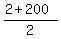 =  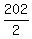= 101 cm.
The amplitude "a" is half the distance between the level 2 cm and 200 cm, or a = 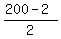 =  = 99 cm.
Since the upper position is at t= 6, I will use the cosine function
y =  +  ,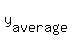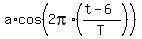
starting my argument (the chronometer) from 6 seconds, where T is the period.
The period value is given as T = 10 seconds, so my final expression for the function is
y = 101 +  .
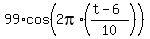In this form, the meaning of each term, parameter and value is visible and understood very well.
You can transform my expression further by any EQUIVALENT way, if you need and if you want.
Solved.
The major things in this analysis is not getting the final expression.
The major thing is to understand what to do with the given parameters.
|
|
|
