Question 1183538: A company that manufactures flash drives knows that the number of drives
x
it can sell each week is related to the price
p
, in dollars, of each drive by the equation
x=1200-100p
Find the price
p
that will bring in the maximum revenue. Remember, revenue (R) is the product of price (p) and items sold (x), in other words, R=xp
Found 3 solutions by ikleyn, ankor@dixie-net.com, Solver92311:
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
A company that manufactures flash drives knows that the number of drives x
it can sell each week is related to the price p, in dollars, of each drive by the equation
x=1200-100p
Find the price p that will bring in the maximum revenue.
Remember, revenue (R) is the product of price (p) and items sold (x), in other words, R=xp
~~~~~~~~~~~~~~~
The revenue is this function of p (of the price)
R(p) = p*x = p*(1200-100p)
It is a quadratic function of p with the zeroes p = 0 and p = 1200/100 = 12.
The maximum of this quadratic function (its vertex) is halfway between the roots at x= 6.
So, the optimal price is p= 6.
The problem is just solved.
----------------
My common sense tells me that the problem's description is DEFECTIVE and must be corrected.
I leave making this correction in your care.
Answer by ankor@dixie-net.com(22740)  (Show Source):
You can put this solution on YOUR website! A company that manufactures flash drives knows that the number of drives x it can sell each week is related to the price p, in dollars, of each drive by the equation x=1200-100p
Find the price p that will bring in the maximum revenue.
:
R = p * x
replace x with 1200-100p
R(p) = p(1200-100p)
R(p) = 1200p - 100p^2
or
R(p) = -100p^2 + 1200p
using the vertex formula: p = -b/(2a) where a = -100, b = 1200
p =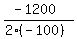 
p = $6 is the price that will give max revenue
Answer by Solver92311(821)  (Show Source):
|
|
|
