Question 1183446: An urn contains 3 red balls, 2 white balls and 1 blue ball. Two balls are drawn without replacement. Let A be the event that at least one ball is red, and B be the event that 2 balls are of different colours.
What is p(A)?
What is p(A|B)
Are events A and B independent?
Found 2 solutions by ikleyn, robertb:
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
An urn contains 3 red balls, 2 white balls and 1 blue ball. Two balls are drawn without replacement.
Let A be the event that at least one ball is red, and B be the event that 2 balls are of different colours.
(a) What is p(A)?
(b) What is p(A|B)
(c) Are events A and B independent?
~~~~~~~~~~~~
(a) Event A is this set of outcomes { (R,W), (W,R), (R,B), (B,R), (R,R) }.
P(A) =  =
=  =  =  .
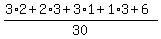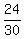(b) Event B is this set { (R,W), (W,R), (R,B), (B,R), (W,B), (B,W) }.
P(B) =  =
=  =  =  .
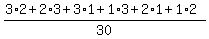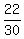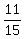The intersection (A and B) is this set { (R,W), (W,R), (R,B), (B,R) }.
P(A and B) =  =
=  =  =  .
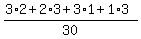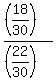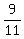THEREFORE, P(A|B) =  =  =  =  . ANSWER
(c) To answer last question, check if P(A and B) is equal to P(A)*P(B).
Solved.
Answer by robertb(5830)  (Show Source):
|
|
|
