An easy way to solve this is to compute
1 - P(complement of indicated outcome)
P(complement of indicated outcome) = P(odd on 1st roll) * P(2 thru 6 on 2nd roll)
= 3/6 * 5/6 = 15/36
and 1 - 15/36 = 21/36 or 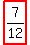
---
A longer way is to recognize that there is overlap between the two cases, and we can break it down to three non-overlapping outcomes:
P = P(odd on 1st roll) * P(1 on 2nd roll)
+ P(even on 1st roll) * P(2-6 on 2nd roll)
+ P(even on 1st roll) * P(1 on 2nd roll)
= (3/6)*(1/6) + (3/6)*(5/6) + (3/6)*(1/6) = (3+15+3)/36 = 21/36 = 7/12, as above.
[ The third term is the case that BOTH rolls produce one of the desired
outcomes. ]
---
Yet another way is to use the inclusion-exclusion principle (we add the two probabilities but, recognizing we've overcounted, subtract out the "common" part which was counted twice):
P = (even on 1st) + (1 on 2nd) - P(even on 1st AND 1 on 2nd)
P = (3/6)+(1/6) - (3/6)*(1/6) = 4/6 - 3/36 = 24/36 - 3/36 = 21/36 = 7/12, as before.