Question 1183394: An artifact was discovered by an archeologist, who initially estimated it to be about 2500 years old. Then, after carbon-14 analysis was completed, it was determined that the carbon-14 contained in the artifact decreased from 20 grams originally to 12 grams now, so that 60% of its original amount of carbon-14 remains. After the mathematical investigation was completed, this model was created: P(t) = 20e-0.00012t, where P(t) is the amount of carbon-14 remaining after 't' years. What conclusion should be made about the age of the artifact?
Found 4 solutions by Boreal, Theo, ikleyn, robertb:
Answer by Boreal(15235)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! p(t) = 20 * e^(-.00012t)
p(0) = 20
p(t) = .6 * 20 = 12
p(t) = e^(-.00012t) = 12
formula becomes:
12 = 20 * e^(-.00012t)
divide both sides of the equation by 20 to get:
12/20 = e^(-.00012 * t)
take the natural log of both sides of the equation to get:
ln(12/20) = ln(e^(-.00012 * t)
since, in general, ln(e^x) = x * ln(e), the formula becomes:
ln(12/20) = -.00012 * t * ln(e)
since ln(e) = 1, the equation becomes:
ln(12/20) = -.00012 * t
solve for t to get:
t = ln(12/20) / -.00012 = 4256.880198 years.
confirm by replacing t in the original equation to get:
p(4256.880198) = 20 * e^(-.00012 * 4256.880198) = 12.
this confirms the value of t is correct.
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An artifact was discovered by an archeologist, who initially estimated it to be about 2500 years old.
Then, after carbon-14 analysis was completed, it was determined that the carbon-14 contained in the artifact
decreased from 20 grams originally to 12 grams now, so that 60% of its original amount of carbon-14 remains.
After the mathematical investigation was completed, this model was created: P(t) = 20e-0.00012t,
where P(t) is the amount of carbon-14 remaining after 't' years.
What conclusion should be made about the age of the artifact?
~~~~~~~~~~~~~
Actually, NOTHING IS farther from the truth than what is written in this post,
and I will explain you WHY - - - right now.
The content of Carbon-14, C14, in the atmosphere is about of 1 - 1.5 atoms per 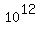 atoms of atoms of
stable Carbon C-12. See this Wikipedia article
https://en.wikipedia.org/wiki/Carbon-14
So, actually, the content of Carbon-14 is tiny percent of Carbon-12, and the content
of these components in any organic on the Earth is in the same proportion.
Therefore, in order for an artifact would contain 20 grams of Carbon-14, its mass
should be many megatons
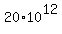 grams = grams = 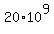 kilograms = kilograms = 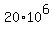 metric tons = 20 megatons. metric tons = 20 megatons.
These numbers shows that the person who created this "problem", is absolutely unfamiliar with the subject.
Yes, the content of Carbon-14 in any artifact is a tiny mass, but it is just ENOUGH for researchers,
armed with relevant modern measurement tools and knowledge to detect it and to make an appropriate analysis.
In our days, hundreds people, hardly familiar with different subjects, position themselves in the Internet
as the "professors", "teachers" or "tutors" without having adequate knowledge.
Learn the subject from good sources, ONLY ( ! )
Answer by robertb(5830)   (Show Source): (Show Source):
|
|
|