SOLUTION: 3cos(7x+1) = 3cos(1)(cos(7x)) - 3sin(1)(sin7x) (ALREADY FOUND BELOW, CANNOT FIGURE OUT THE SECOND ONE) 3sin(5x+3) = 3sin(3)(cos(5x)) + 3cos(3)(sin5x) Now reverse these formulas a

Algebra ->  Trigonometry-basics -> SOLUTION: 3cos(7x+1) = 3cos(1)(cos(7x)) - 3sin(1)(sin7x) (ALREADY FOUND BELOW, CANNOT FIGURE OUT THE SECOND ONE) 3sin(5x+3) = 3sin(3)(cos(5x)) + 3cos(3)(sin5x) Now reverse these formulas a      Log On


   

Question 1183393: 3cos(7x+1) = 3cos(1)(cos(7x)) - 3sin(1)(sin7x) (ALREADY FOUND BELOW, CANNOT FIGURE OUT THE SECOND ONE)
3sin(5x+3) = 3sin(3)(cos(5x)) + 3cos(3)(sin5x)
Now reverse these formulas and given the expanded version find the version with just one term. This involves solving a pair of equations -- in order to get Acos(x) +Bsin(x) = Rsin(x+b) = Rsin(b)cos(x)+Rcos(b)sin(x) what values must you choose for R and b? (Match coefficients.)
By convention we'll assume that the amplitude (the first coefficient on the left hand side) is positive.
__7___ cos(7x+__-1/7___) = 7cos(7x)+1sin(7x)
_____sin(5x+______)=6cos(5x)=-3sin(5x) <-- NEED THIS ONE SOLVED
Found 2 solutions by Edwin McCravy, EdwinMcCravy:
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
The problem is that you have this:

_____sin(5x+______)=6cos(5x)=-3sin(5x)
 
but cross%286cos%285x%29=-3sin%285x%29%29 is false!!!

Edwin

Answer by EdwinMcCravy(4) About Me  (Show Source):
You can put this solution on YOUR website!
You typed this:

_____sin(5x+______)=6cos(5x)=-3sin(5x)
but I don't think you meant to type =-
I think you might have meant this instead:

_____sin(5x+______)=6cos(5x)+3sin(5x)
Put A in the first blank and C in the second:

A%2Asin%285x%2BC%29%22%22=%22%226cos%285x%29%2B3sin%285x%29

Use the identity sin%28alpha%2Bbeta%29=sin%28alpha%29cos%28beta%29%2Bcos%28alpha%29sin%28beta%29

A%2A%28sin%285x%29cos%28C%29%5E%22%22%2Bcos%285x%29sin%28C%29%29%29%22%22=%22%226cos%285x%29%2B3sin%285x%29

Distribute the A

A%2Asin%285x%29cos%28C%29%2BA%2Acos%285x%29sin%28C%29%22%22=%22%226cos%285x%29%2B3sin%285x%29

For this to be an identity and true for all x, the term on the left that
contains sin(5x) must equal the term on the right that contains sin(5x). So:

A%2Asin%285x%29cos%28C%29%22%22=%22%223sin%285x%29

Divide both sides by sin(5x)

A%2Acos%28C%29%22%22=%22%223

Now we'll do it for the other two terms
{
{{A*sin(5x)cos(C)+A*cos(5x)sin(C)}}}%22%22=%22%226cos%285x%29%2B3sin%285x%29

For this to be an identity and true for all x, the term on the left that
contains cos(5x) must equal the term on the right that contains cos(5x). So:

A%2Acos%285x%29sin%28C%29%22%22=%22%226cos%285x%29

Divide both sides by cos(5x)

A%2Asin%28C%29%22%22=%22%226

Divide equals by equals

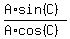
%28A%2Asin%28C%29%29%2F%28A%2Acos%28C%29%29%22%22=%22%226%2F3

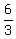Cancel the A's

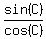
sin%28C%29%2Fcos%28C%29%22%22=%22%222

tan%28C%29%22%22=%22%222

So C is the angle whose tangent is 2 

So C = arctan(2)

We draw a right triangle that has contains angle C.  Since we know that
tangent = opposite/adjacent, we draw the side opposite C as 2 and the side
adjacent to C as 1.  Then we can use the Pythagorean theorem to find the
hypotenuse:





Since A%2Acos%28C%29%22%22=%22%223

Then from the triangle, cos%28C%29=adjacent%2Fhypotenuse=1%2Fsqrt%285%29

A%2Acos%28C%29%22%22=%22%223
A%2A%281%2Fsqrt%285%29%29%22%22=%22%223
A=3sqrt%285%29

So the answer is:

3sqrt%285%29%2Asin%285x%5E%22%22%2Barctan%282%29%29

[Let me know in the space below if this was not what you meant instead of what
 you typed.  If you do, I'll get back to you by email.]

Edwin